Review of Uncertainty by Briggs

7/6/19

This is a book review of Uncertainty: The Soul of Modeling, Probability & Statistics by Briggs. Also, check out Brigg's website at wmbriggs.com. Ok, on to the review. Briggs' quotes are in blue.

Causality

Throughout the book, Briggs talks about causality. I'd say, however, that a statistician's interest is most often seeing if an effect is real, which is slightly different. Also, saying "due to chance" is not claiming randomness is a force, or energy, or material, but is just shorthand/speech for saying observations are consistent with a proposed model.

"...there are people who think statistical models prove causality..." A common thing you'll find in this book is Briggs talking about "proof" and "truth" and "known" instead of "evidence for". Most people in science do not talk about absolute proof but only evidence.

Randomness

"...there are people who think...that randomness is magic..." I must say, literally no one I know of thinks that randomness is magic. Saying something is magic is a tactic to dismiss something as silly. For example, magicing dead people back to life.

I read this fascinating paper recently. It talks about a method of ensuring survey respondent privacy ("differential privacy", see The Algorithmic Foundations of Differential Privacy), which is being used more and more in government and private industry. They said "Randomization is essential; more precisely, any non-trivial privacy guarantee that holds regardless of all present or even future sources of auxiliary information, including other databases, studies, Web sites, on-line communities, gossip, newspapers, government statistics, and so on, requires randomization." The DIEHARD tests also come to mind as useful things involving pseudorandomness, as do some blockchain verification methods.

Briggs can argue that writing against causality is self-defeating (because there is cause in writing a book), but then one can just argue that arguing against writing against causality is self-defeating because the jury is still out on if randomness exists. Perhaps randomness in our universe's formation, or at the quantum level, or random mutations, allowed book writing entities to form and write books arguing for causality and against randomness? The hypothetical game is pretty easy to play. Or perhaps there is a combination of causality and randomness in the universe, which seems more likely in my opinion.

Fairness

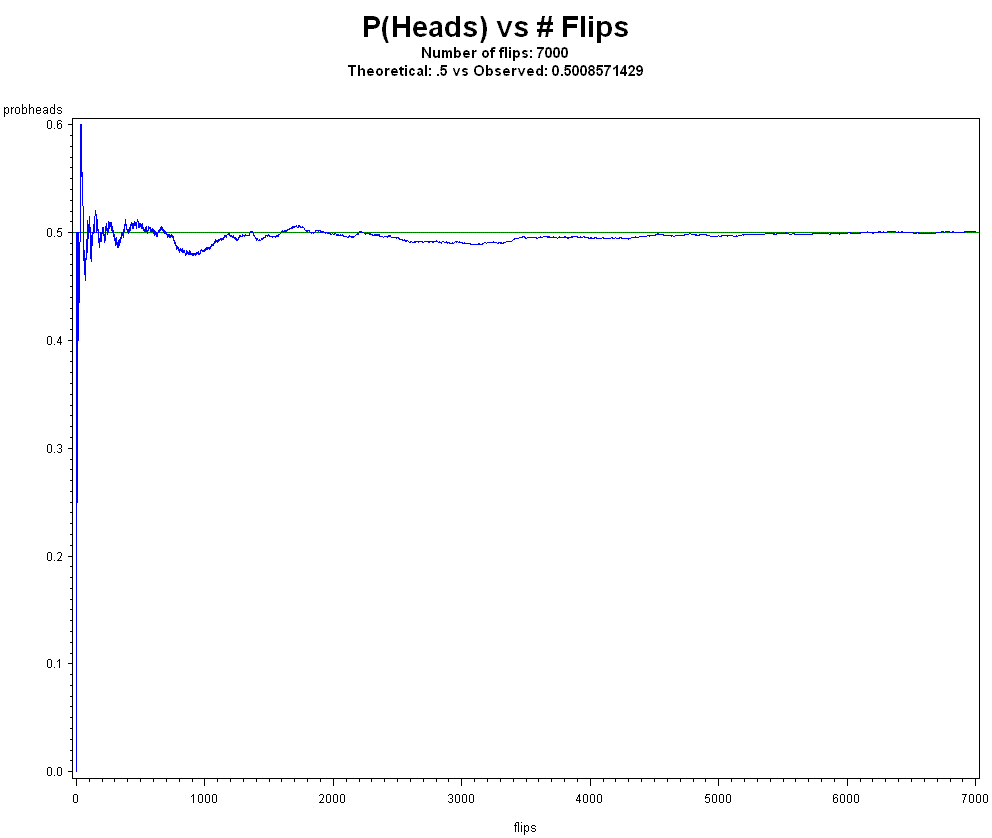
"fair, what else can it mean but to claim that each side is perfectly symmetric, even down to the quantum level". This is done by goodness of fit tests, comparing expectations from a sensible model to observed data.

I'll say that if the true probability of heads (which no one ever knows) is .50 and I estimate it from sound experiments to be .4999999991, I will not lose an iota of sleep, much like engineers who use a few digits of pi in their calculations. This is a common argument Briggs makes, that one needs to prove something exact, or have an actual infinity. In reality, no branch of any science can do this and it is a strawman argument. Casinos and lotteries are a treasure trove of empirical evidence of demonstrating the fairness of physical objects.

Say you have a die and the relative frequencies look like they are converging on 1/6. Now you cut a small chunk off of a corner. After some trials, you find that this changes the relative frequencies away from 1/6. This suggests that probability is a physical trait and not as Briggs suggests in the mind. One could also design say a dice rolling or coin flipping robot and have it record frequencies. These frequencies too will converge with no human mind involved.

Briggs' example using a number between 2 and 12 inclusive (I'll call that "this event") being P(this event) = 1/11 in one setting and P(this event) = 1/36 in another setting being evidence against probability being physical is not convincing. It is not because, as even Briggs says, probabilities are conditional (or as I would say, we speak of probabilities within a reference class). In the first case, it is P(this event|rule set 1). In the second case, it is P(this event|rule set 2). The two conditions or reference classes are different. Briggs has admitted with this example that the sample space does matter, actually providing an argument for the frequentist approach.

Parameters

The average weight of an adult person in the United States when you get to the period at the end of this sentence is W₁. That W₁ is reality, since weights are reality, and average weights are reality, but one could not observe it, because we could not literally go out and weigh each and every person. It is a parameter, and parameter is to population what statistic is to a sample (parameter:population::statistic:sample).

"This alone will go miles toward eliminating the so-called replication crisis." Briggs offers no evidence that eliminating talking about parameters will have an effect on experiments not replicating.

Frequentism

Briggs, like other critics of frequentism, makes the mistake of giving examples where frequentist probability cannot explain some type of uncertainty well. However, frequentism purposely limits probability to mean a certain thing (convergence of relative frequency, irrelevance of place selection) like many branches of science limit what they are studying (geology doesn't specialize in bones and archeology doesn't specialize in rocks). Some examples Briggs gives of chance or uncertainty wouldn't even be claimed by frequentism as being probability in the first place.

If Briggs believes something like a relative frequency would settle down to say .60 after say 100,000 trials, but then suddenly go to .20 in a limit, the onus is on Briggs to explain a) what math would explain this and go against the Strong Law of Large Numbers (SLLN), and b) why we don't observe this empirically or why we should believe that could happen. The SLLN says that it is almost certain that the relative frequency of Heads will remain near the fixed value p, whatever p may be (ie. doesn't have to be 1/2), and be within the interval [p-e, p+e], for any small e > 0, provided sufficiently large n. This is both a mathematical and empirical law.

Briggs gives no evidence for the claim "...eliminate hypothesis testing, which serves merely to affirm biases, would go far to improve the decisions resting on probability."

"...there are people who think...that p-values validate or invalidate theories..." No one thinks that p-values all by themselves do such a thing. If you have a well-designed experiment, background knowledge, set alpha by cost or sample size, multiple adjustments, and then repeat the experiment, rule out questionable research practices, and then still get small p-values, then it does establish an effect. If one regularly observes greater than 90 heads when flipping a coin 100 times, this is very strong evidence that p is greater than .50. Why wouldn't it be?

"The student...is encouraged not to ask too many questions but instead to calculate, calculate, calculate." And some hypothetical students are encouraged to ask many questions.

"...tools which appear 'good enough' because everybody else is using them." Actually, the tools of standard statistics are good because they work well and everybody else is using them because they work well. Briggs needs to show his proposed methods work well.

"...limiting relative frequency is of no use..." Then why do frequencies work so well and are used all over the world in sciences and other areas? Why do Bayesians, propensity, and logical probability exponents regularly use frequencies (histograms, counts) if frequencies are of no use? Long ago, Poisson and Boole uses frequencies as inputs to their work. Why is that? Why do the Strong Law of Large Numbers (SLLN) and the Central Limit Theorem (CLT) exist? Why did Kolmogorov rest his measure theoretic axioms on von Mises' collective? Why does flipping a coin make the relative frequency of heads seem to converge to a flat line for anybody? These are questions Briggs has not convincingly addressed in my opinion.

"Chance and randomness are not mystical entities or causes; they are only other words for ignorance." I've already addressed the mystical or magical bit. As far as chance and randomness being other words for ignorance, that is debatable, maybe just semantics. I'd say assuming a probability distribution is just imposing some type of structure as a model. Is using a model ignorance? Maybe. But if models are ignorance, why do they work pretty well? Maybe only partial ignorance. But isn't partial ignorance also partial knowledge?

Despite Briggs' repeated insistence, there's nothing that confusing about frequentism nor p-values if you understand them. But in any case, misuse or misapplication is no reason to throw the error control baby out with the misuse bathwater. When doing research on this article, I found a video of Briggs on YouTube titled "Statistical Follies and Epidemiology. William "Matt" Briggs, Ph.D." where he says no one can ever remember what a p-value is, etc. However, someone in the audience actually had a semi-decent response at around 33 minutes in. The man essentially said that the p-value is a function of the distance the observed test statistic is from what you'd expect from the model, and that as the distance gets larger the p-value gets smaller. Briggs just moves on, continuing his no one can ever remember schtick. In my search I also found A case study of the tactics of climate change denial, in which I am the target by Phil Plait (The Bad Astronomer), that discusses an exchange he had with Briggs, which was an interesting read.

The logic of modus tollens says: P->Q, and if we observe not Q, therefore we conclude not P. We assume a fair coin model. We expect about 500 heads if we flip a coin 1,000 times. However, from a well-designed experiment we observe 900 heads (900 put on a p-value scale would be an extremely small p-value). Therefore, we conclude the fair coin model is not good here. Briggs would need to explain convincingly why this reasoning is erroneous and give a model that works better.

"Classical hypothesis testing is founded on the fallacy of the false dichotomy. The false dichotomy says of those hypotheses that if one hypothesis is false, the other must be true.". Again we see the "true" bit when science just talks about "evidence". Actually, hypothesis testing divides up the parameter space into say two mutually exclusive and exhaustive parts. If we have evidence to conclude it is not in one part, then we must conclude it is in the other part. Also, we allow errors (Type 1, Type 2), so we are definitely not saying any decision is we make from the evidence is "true" in any absolute sense.

Regarding frequentism requiring infinity, and there is no actual infinity to observe in real life, etc., this is not correct, as infinity and frequentism are wrong but useful models. Things like areas under curves work by modelling smaller and smaller rectangles under a curve ("but we never observe those in real life!" Briggs might say), yet integration works. It does because it is a model, and your computer does it until the successive changes between computed areas is less than an epsilon. In our finite world, we can say that for any very small d>0, if, at the end of n trials, |f_n-p| < d, then we are justified in saying f_n~p (read "f_n is approximately p") for all intents and purposes. If the "true" p, which we never know, is .50, for example, do you worry if the observed relative frequency is .4999999999 or .500000001?

Briggs mentions the finiteness of the universe as some evidence against literal infinity. Minor point, but I'd just like to mention that all we know about is the observable universe. Briggs mentions that no one can really imagine an infinity even though they say they can, yet Briggs talked about the infinite number of numbers between 0 and 1... so can he do it or use a infinity as a model but no one else can?

In one example, Briggs needed a large N for an argument, so he decided to make it "a googolplex to the power of a googolplex to the power of a googolplex, 84 times, which is a mighty big number, but finite". I'm glad Briggs sees the value of frequentism and large-N arguments. Maybe Briggs can imagine a googolplex to the power of a googolplex to the power of a googolplex, 84 times, but not infinity, which is still pretty impressive I'd say. Perhaps Briggs can explain why we'd expect the relative frequency of Heads to be around .50 for a googolplex to the power of a googolplex to the power of a googolplex, 84 times number of flips, but not be around .50 after that?

Regarding frequentism hypothesis testing requires H₀ to be exactly true, nothing requires any model to be exactly true outside of the mathematics. If any assumptions do not hold exactly in reality, there are the fields of robust and nonparametric statistics which can address these issues. There is also, quite simply put, an allowance for making errors; alpha, beta, etc.

I can think of several ways one could reasonably model the darts player improving over time (logistic regression or time series come to mind). I'm not sure why Briggs thinks this is a good example for the inadequacy of frequentism from Hajek.

Briggs talks about Keynes and "weight of probability", and Keynes saying "new evidence will sometimes decrease the probability of an argument, but it will always increase its weight". This feeling is explained in my opinion by the Strong Law of Large Numbers with relative frequencies being calculated as well as variances getting smaller, as well as observing results from well-designed experiments over time.

I would also side with Bayesians and conclude that assuming a uniform distribution or something uninformative is a reasonable way in most cases to proceed (although not perfect, which has never been claimed in the first place, and does have flaws). Briggs is wrong when he says that "there cannot be an equal probability for infinite alternatives because the sum of probabilities, no matter how small each of the infinite possibilities is, is always (in the limit) infinity" because a) the continuous uniform distribution is only a wrong but useful model, and b) the "infinite possibilities" are in reality only finite and limited by the digits the computer is showing you.

"You give this pill to 100 volunteer sufferers, and to another 100 you give an identical looking placebo. ... 71 folks in the profitizol group got better, whereas only 60 in the placebo group did. Here is the question: in what group were there a greater proportion of recoverers? ... the untrained...civilian will say 'The drug group', which is the right answer." This confuses a sample with a population in my opinion. Briggs only has one sample, from one experiment, and a point estimate. He can only say descriptively that more recovered in the drug group in this sample, not that overall the drug is effective, which is what generally science aims to establish.

Miscellaneous

"Truth resides in the mind..." Again, the "truth" bit. I would opine that science does not talk about "truth" or "proof" but only "evidence". Anyway, the funny thing about minds is that they can get fooled by optical illusions, magic, overconfidence, etc. Briggs also does not convincingly distinguish mind from the physical organ called the brain or functions of it.

"all probability is conditional" I don't actually think anyone would disagree. Briggs stating that all probability is conditional is not new. The idea of a reference class in frequentism, for example, is well-known since at least Venn's time. If one writes P(Heads), I don't believe they are literally claiming, as Briggs suggests, that nothing is involved with Heads occurring. I believe rather the opposite, that they are saying it is conditional on everything, which is kind of like saying all those things do not really matter to explicitly list because they all matter. For example, instead of writing probabilities like P(A|stuff here), one could just let B = A|stuff here, and write P(B). Even Briggs would probably agree that there could be too much "stuff here" to list, so what guidelines does Briggs have for constructing such a list? He doesn't say.

Regarding P(Heads|X) and P(Heads|Y), if X and Y are "dime" and "quarter", the probabilities are probably the same. If X and Y are "flipping on a table" and "flipping into glue", or utilizing different flipping methods, maybe the probabilities differ. If you have reason to believe the probabilities differ some way, you explicitly list and X and Y. Also, one could design an experiment to determine if there are differences due to various conditions.

Briggs discusses the Monty Hall problem. In my opinion, one can describe and solve the Monty Hall problem better using sample spaces. One can also simulate and solve the Monty Hall problem using random numbers and see the relative frequencies converge quite easily.

I found several instances of Briggs engaging in poisoning of the well, by saying things like "God rot them" (on p-values), "Die, die die" (on p-values), and refers to parameters as "creatures". This is entertaining but not a convincing way to argue a point.

"This isn't a recipe book." That's too bad. If it was, maybe it would provide some concrete things one could do to solve even very simple problems, and might be relied upon all over the world the way frequentism and hypothesis testing are. The reader should be asking themselves "Why is there not easy-to-use-out-of-the-box software for this approach?"

In doing research for this article, I found out that on his website Briggs has code for doing some of what he claims his method can do. Of course, the code uses regressions, MCMC, Stan, survival analysis, and histograms (his y being discrete). This is not moving away from parameters and models and random numbers but relying on them. There is also no guidance for interpreting the changes in predicted probabilities, if they are statistically or practically significant, other than "it depends on the decision maker". You know what, it does with frequentism too, that is why there is alpha and smallest effect sizes of interest (SESOI), for example. But Briggs will leave that "as homework". How about since it is Briggs' approach that he is trying to convince us of, that Briggs does the homework?

"Bayes is not what you think." I'm not sure how to parse this. How does Briggs know what any reader thinks?

"Probability is not decision." This is semantics in my opinion. Probability (or more properly we should say results from well-designed and repeated experiments) is used to make decisions.

"Probability presupposes truth; it is a measure of characterization of truth..." Again, the "truth" bit. However, this admits that parameters are indeed real if you view a population parameter as an underlying truth that statistics estimate.

"Can we know truths? Yes. And if you disagree you necessarily agree." Sure I can disagree, because I'm not sure Briggs has defined "know" or "truth" very well to begin with. I can estimate the value of a parameter, or at least estimate the value of a parameter at time t. Does Briggs mean something other than estimate and parameters when he talks about "know" and "truth"? And is his definition of "truth" always fixed forever or can it evolve over time (like say if the speed of light very, very, very slowly changes)?

"...just because a statement is mathematically true does not mean that the statement has any bearing in reality." This makes sense, but it doesn't mean it doesn't have any bearing either. Note how we can make many logical statements that have nothing whatsoever to do with actual reality.

"...there are plenty of necessary truths we know...'God exists' is another: those who doubt it are like circle-squarers..." OK, I'll bite. I am not into trying to square circles, but I am skeptical that any god(s) (Briggs hasn't even defined what he means by "God") exist. I'm open to the possibility, but it is up to believers to supply the evidence for their claims.

"That radium does not have the atomic weight of w might be false, if the equipment, no matter how sophisticated or fine, erred in its measurements." That may be, but Briggs would have to then explain why we should expect all of these machines and scientists the world over to err in their measurements. If the true atomic weight is w (and again, we probably never know the truth - but Briggs still hasn't defined "know" and "truth"), but we measure w_t at time t, Briggs may say "gotcha!". Whereas science maybe says, w_t is confirmed by multiple scientists, labs, in different countries, and over different time periods, and sees that the difference |w-w_t| gets smaller in general over time.

"This [Scientism] is the false belief that the only truths we have are scientific truths." Science does not talk about "truth", but only evidence. I would say science is the best tool for the job that we know of for obtaining this evidence. And yes, "self-correcting" obviously "implies it [science] errs", because that is what science is about and is really no big deal to make mistakes that we learn from. You'll rarely find any religion admitting error. I'm not saying science must be used for everything, but if Briggs has another method that produces more reliable evidence of how the world works, I'd like to know.

"e.g., 'God does not exist'" Actually, a skeptic would probably not make that claim at all, but rather state that 'there is no evidence for the claim of god(s) existing', 'there is no evidence for claimed miracles', etc. Briggs also apparently writes for the Christian inspiration site Stream.org, of which mediabiasfactcheck.com noted "...we rate The Stream a moderate Conspiracy website based on promotion of right-wing conspiracies and a strong Pseudoscience site for promotion of climate change denial and creationism, as well as non-scientific information regarding homosexuality". Unfortunately for Briggs, belief, no matter how strong, is not evidence.

I've discussed his argument against trends previously.

Briggs also contributed his method of statistical analysis to Sidney Powell and in blogs that were used to bolster the false claims of 2020 election fraud. These false election fraud claims were endlessly repeated by Trump, Sidney Powell, Rudy Giuliani, Qanon, Stop the Steal, rioters at the Capitol, and many others. The picture below from a court document sums up this work:

Perhaps now instead of his self-proclaimed "Statistician to the Stars" title he can be the "Krakenstician" or the "Krakenstician to the Stars"?

My Summary

If the claim of logical or predictive probability being superior to frequentism or Bayesian approaches or can solve more problems is to be taken more seriously, it is not enough to pray the world stops using frequentism and Bayesian methods to solve problems. Briggs would need to create software tools to do what he writes so very enthusiastically about, and show that it produces better results than the standard theory and tools that exist, and do it not using the very things (like randomness and parameters) that he critiques from the standard approaches. I humbly suggest starting with the common problem of comparing two samples to see if the populations they come from are different on some variable.

Interestingly enough, in Briggs' The MIT Dahn Yoga Brain Respiration Experiment articles, he discusses a test he had designed to test the psychic claims of some Korean children. He used randomization, alpha, and p-values to do it. Briggs is trying to convince you that pseudorandom numbers, alphas, and p-values can't possibly work for you or for science, but they worked extremely well for "pre-Damascus road conversion" Briggs here.

Despite my criticisms of its very unconvincing criticisms on frequentism, Bayesian, randomness, parameters, and science, I recommend this book because it is entertaining and does get one thinking deeper about logic, probability, and statistics. However, I personally do not expect the world to return to the time of Aristotle and Aquinas and talk about "essences" and "natures" ever again.

I would strongly recommend Briggs read Statistical Inference as Severe Testing: How to Get Beyond the Statistics Wars by Mayo.

Thanks for reading.