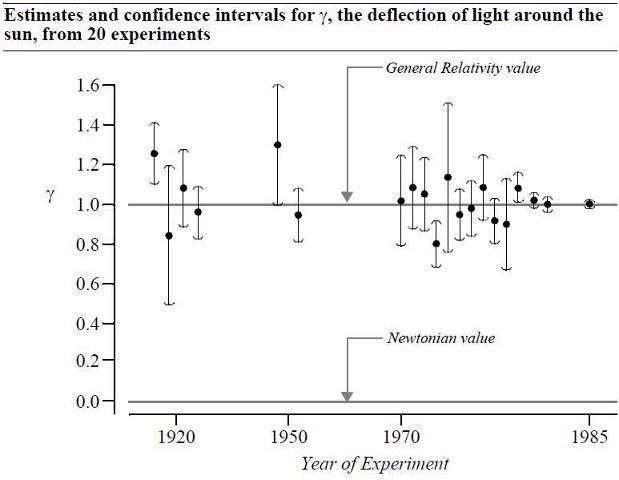
It's Time to Retire the Retire Statistical Significance Articles

6/4/19

Check out the 6/3/19 Altmetric blog and podcast here. In it, Lucy Goodchild discusses significance testing and interviews Blake McShane, who discusses arguments against alpha, p-values, statistical significance, and frequentism. I discuss arguments against frequentism and related topics in my Objections to Frequentism. In this article, I look at some of the blog and podcast talking points.

First, setting alpha is not, or should not be, "arbitrary", as is being claimed. Alpha is the probability of making a Type 1 error, and should be set based on the cost of making a Type 1 error for your study, as well as perhaps based on the sample size in your study. Of course, and they don't mention this here, a cutoff for determining "significant" Bayes factors runs into the same charge of being arbitrary.

Regarding "as Prof McShane and his colleagues explain in their paper, there's no ontological reason or basis for such a sharp threshold" of alpha = .05, that does not mean there are no good reasons period. Fisher basically said it was convenient, and resulted in a z-score of about 2, and made tables in his books (pre-computer) easier. The use, as Fisher knew and wrote about, more importantly roughly corresponded to previous scientific conventions of using probable error, or PE instead of standard deviation or SD. The PE is the deviation from both sides of the central tendency (say a mean) such that 1/2 of the observations are in that range. Galton wrote about Q, the semi-interquartile range, defined as (Q3-Q1)/2, which is PE, where Q3 is the 75th percentile and Q1 is the 25th percentile. For a normal distribution, PE ~ (2/3)*SD. Written another way, 3PE ~ 2SD (or a z-score of 2). The notion of observations being 3PE away from the mean as very improbable and hence "statistically significant" was essentially used by De Moivre, Quetelet, Galton, Karl Pearson, Gosset, Fisher, and others, and represents experience from statisticians and scientists, and not something pulled out of thin air. See On the Origins of the .05 Level of Statistical Significance by Cowles and Davis.

Second, if an arbitrary p-value "determines if a study is published or not", that is not an argument against alpha and p-values and significance testing and frequentism. That is an argument against arbitrary journal standards.

Third, regarding the "replication crisis", this is a misnomer. If a second study does not find statistical significance but a similar first study did, this is not a crisis. This is actually a good result for science. This is just a result of working with data. Doing more well-designed studies will help lead us toward evidence for an effect or not. But by the way, this "second study not significant but first study significant" could also happen using Bayes Factors or other approaches. I'd actually be interested in the results from not only the first and second, but also the third, fourth, fifth, etc., experiments.

Fourth, regarding 850 signatories. Is that impressive? I have no way of knowing. Let's try and determine for what value of X, where X is the number of signatories, is it impressive? If only we had some way of determining this... Oh, let's also see the number of scientists who favor significance testing. They do not say. But they do essentially say (see the "Ninth" point) the number using it doesn't really matter.

Fifth, the fact that not rejecting H₀ does not prove H₀ true is well-known. However, this is also somewhat of a strawman, as no one has ever talked about "proof", rather only evidence. I'd argue that many well-designed studies not rejecting H₀ can be evidence for H₀ being true.

This is not evidence for H₀: gamma = 1?

Sixth, such articles keep harping on interpreting results from single studies. Fisher himself said to do more than one experiment. Single studies will not show much of anything using any approach, only an "indication". This is why replicating (as in repeating, not necessarily getting the same result as a previous study) experiments and meta analysis are important. The mentioned "file drawer problem" with meta analysis can also happen with other approaches.

Seventh, regarding presenters saying "there is no difference between groups". Let's break this down. Let's first distinguish between "no difference at all" and "no difference using this alpha level". Surely those are different statements. Let's also distinguish between sample and population. Surely the presenters are not saying there is no difference between the sample statistics, since a mean of 8.7 and a mean of 7.3 are different. They are quite obviously saying the observed sample data (means and variances) do not indicate a difference in the population parameters. And again, this statement is predicated on the assumptions of the models and alpha level.

Eighth, regarding "errors are widespread" with significance testing. So are we to believe that the same people that are confused with hypothesis testing will not make errors with the intricacies of prior selection and Markov Chain Monte Carlo (MCMC) settings? To paraphrase Mayo, let's not throw the error control baby out with the misuse bathwater. Also, please check out Mayo's Statistical Inference as Severe Testing: How to Get Beyond the Statistics Wars for extremely detailed discussions of these issues.

Ninth, regarding the "it's taught because it's used and it's used because it's taught" circularity problem to "explain" the popularity of significance testing. Actually, it is taught because it works and it is used because it works. That was easy to clear up.

Tenth, regarding "creates a problem in science". Actually, statistics of the frequentist sort have been quite good for science. I discuss more here, but a short list is: experimental design, survey sampling, and quality control. Also, modus tollens logic, which significance testing uses, is falsificationist, and is a good approach to science.

Eleventh, they do not detail any cons of the proposed vague and unproven alternative approaches. For example, how would our knowledge change if instead everyone uses their own subjective Bayesian prior to determine "truth"? Would it change for the better?

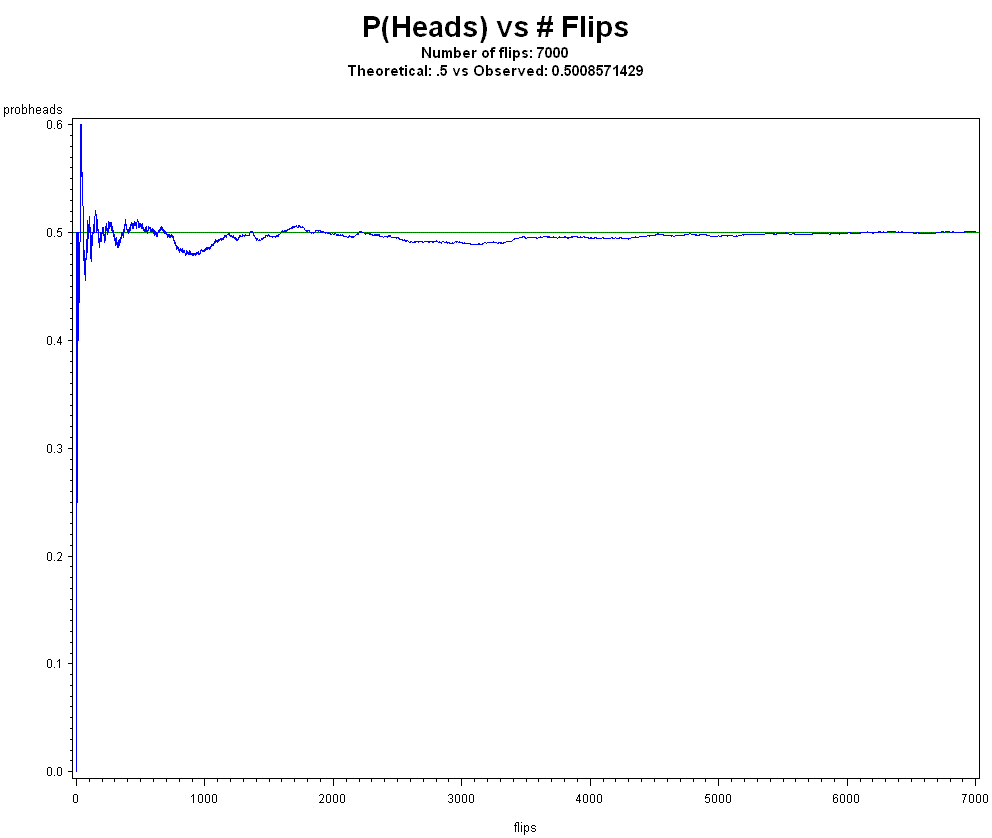
Twelfth, regarding the "not even scientists can explain p-values because they are highly counterintuitive" argument, nothing could be further from the truth. Many scientists can in fact explain p-values. Also, a distance a test statistic is away from a proposed model is quite intuitive. If you model a coin as fair, and you flip a coin 10,000 times, you'd expect about 5,000 heads. If you get 9,000 heads, which is the same as saying a small p-value, this is good grounds for rejecting the fair coin model.

Not intuitive?

Thirteenth, they need to read about equivalence testing, where you set the smallest effect size of interest (SESOI), and look not only at statistical significance but also practical significance. See Equivalence Testing for Psychological Research: A Tutorial by Lakens et al.

I'm thrilled that they got some eyeballs on their articles and increased their metrics and Bayesian point scores. I'm not thrilled to see the same poor arguments against significance testing being rehashed over and over.

Thanks for reading.