Email news@statisticool.com to sign up to receive news and updates
Coin Flipping in Python
7/18/19
As I note in Objections to Frequentism
The Strong Law of Large Numbers (SLLN) says that it is almost certain that between the mth and nth observations in a group of length n, the relative frequency of Heads will remain near the fixed value p, whatever p may be (ie. doesn't have to be 1/2), and be within the interval [p-e, p+e], for any small e > 0, provided that m and n are sufficiently large numbers. That is, P(Heads) in [p-e, p+e] > 1 - 1/(m*e2).
I showed this in an Excel spreadsheet here. In this article, I share Jupyter notebook code I wrote to carry out this "coin" flipping in Python.
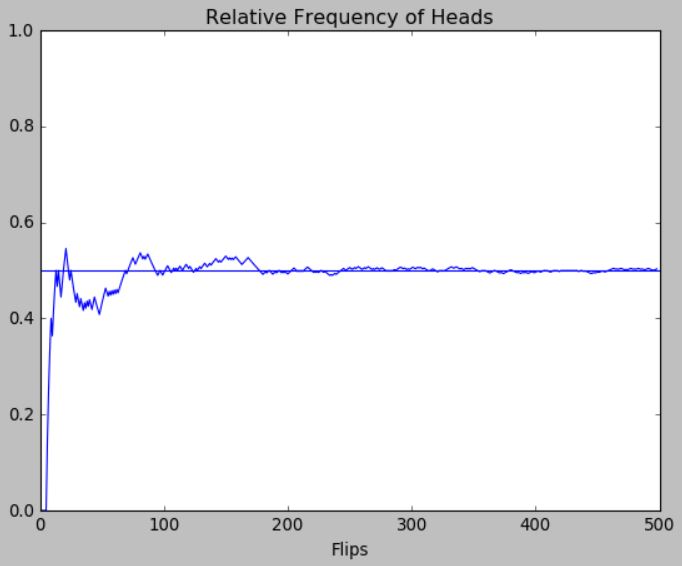
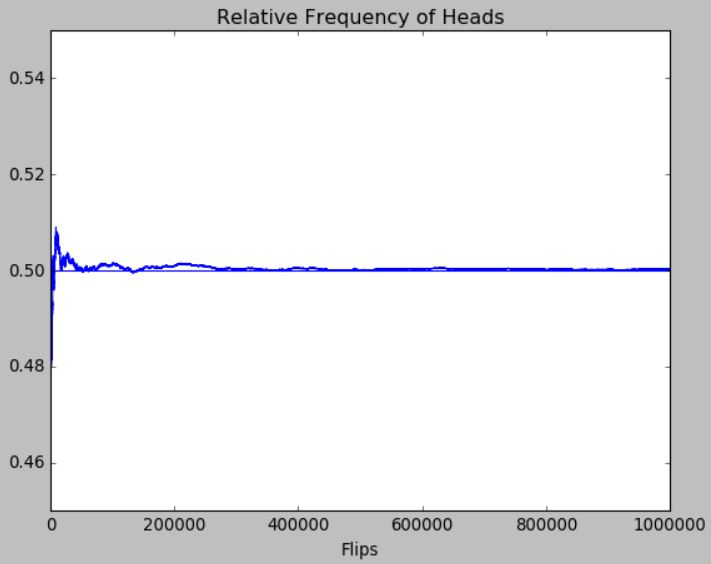
Here are examples from flipping 500 and 1,000,000 times. For the larger number of flips, note that I zoomed in on the Y-axis
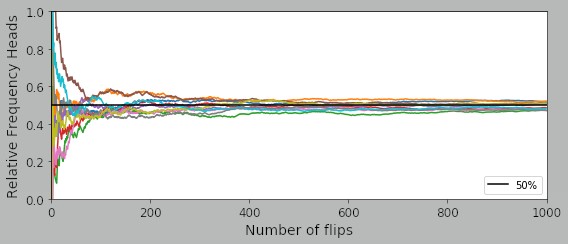
One can also flip several coins at once. Here I show 1,000 flips using 10 coins
Does this behavior happen for real coins or other objects (dice, tacks, playing cards, balls drawn from an urn)? The answer is...go try it.
Thanks for reading!
Please anonymously VOTE on the content you have just read:
Like:Dislike:
If you enjoyed any of my content, please consider supporting it in a variety of ways:
- PLEASE take a moment to check out two GoFundMe fundraisers I set up. The idea is to make it possible for me to pursue my passions. My goal is to be able to create free randomized educational worksheets and create poetry on a full-time basis. THANK YOU for your support!
- Email news@statisticool.com to sign up to receive news and updates
- Donate any amount via PayPal
- Take my Five Poem Challenge
- Subscribe to my YouTube channel
- Visit my Amazon author page
- Buy what you need on Amazon using my affiliate link
- Follow me on Twitter here
- Buy ad space on Statisticool.com
AFFILIATE LINK DISCLOSURE: Some links included on this page may be affiliate links. If you purchase a product or service with the affiliate link provided I may receive a small commission (at no additional charge to you). Thank you for the support!