Clayton's Fallacy
7/16/21
This article is a review of the book Bernoulli's Fallacy: Statistical Illogic and the Crisis of Modern Science by Clayton. Also, check out Clayton's website at aubreyclayton.com.
Objections to Frequentism
I wrote Objections to Frequentism in response to reading poor criticisms of frequentism (some of them contradicting) that get rehashed year after year. Many, if not all, of Clayton's objections have been covered in this collection. Please, check out the resources in that longer article too. On Clayton in particular, I also wrote The Flawed Reasoning Behind The Flawed Reasoning Behind the Replication Crisis in response to Clayton's The Flawed Reasoning Behind the Replication Crisis. Also, see a similar critique of Kurt's article Technically Wrong: When Bayesian and Frequentist methods differ at Bayesianly Wrong.
Ok, on to the review of "Bernoulli's Fallacy".
Bernoulli's Fallacy
The main point of this book is what Clayton calls "Bernoulli's Fallacy". This is, if D = data, and H = hypothesis, then confusing P(D|H) = P(H|D), or using "only sampling probabilities", or basically Clayton's vision of frequentist statistics. Any of these are "Bernoulli's Fallacy", by Clayton.
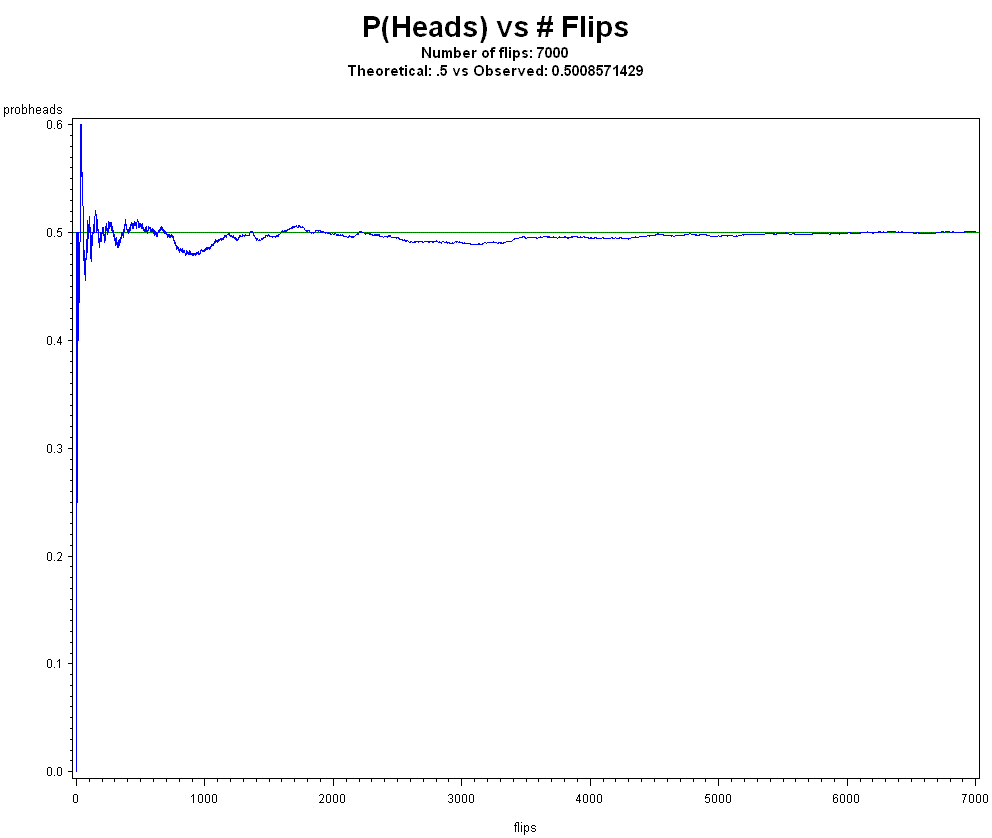
Since antiquity, and formally since at least the 1500s, Cardano and others noticed that as more observations were collected, the more accurate your estimates seemed to get, on average. Bernoulli, in the early 1700s, derived what is called the Weak Law of Large Numbers (WLLN) that explains this basic idea mathematically. Over time, this was extended to be more mathematically rigorous with less restrictive settings and stronger convergence, to give us the Strong Law of Large Numbers (SLLN).
Venn discussed that the WLLN kind of does not apply to all real life events, and von Mises wrote that WLLN is purely arithmetic and some sequences of data don't apply (for example, sequences where place selection is relevant) so WLLN cannot serve as a definition for probability. I agree with Clayton's argument that frequentists believe a convergence theorem underpins a part of statistics in some way. I disagree that WLLN/SLLN are fundamentally flawed for analyzing the world.
Clayton correctly points out that if the X's are from a Cauchy distribution then the WLLN fails to converge. We cannot, however, make the leap to saying the WLLN is flawed or frequentism is flawed because of this. In fact, the WLLN requires the mean to be finite, and there's some conditions on variance as well. In most real life situations we encounter, IID is a good approximation and means are finite. Also, in real life we almost never know the true underlying F.
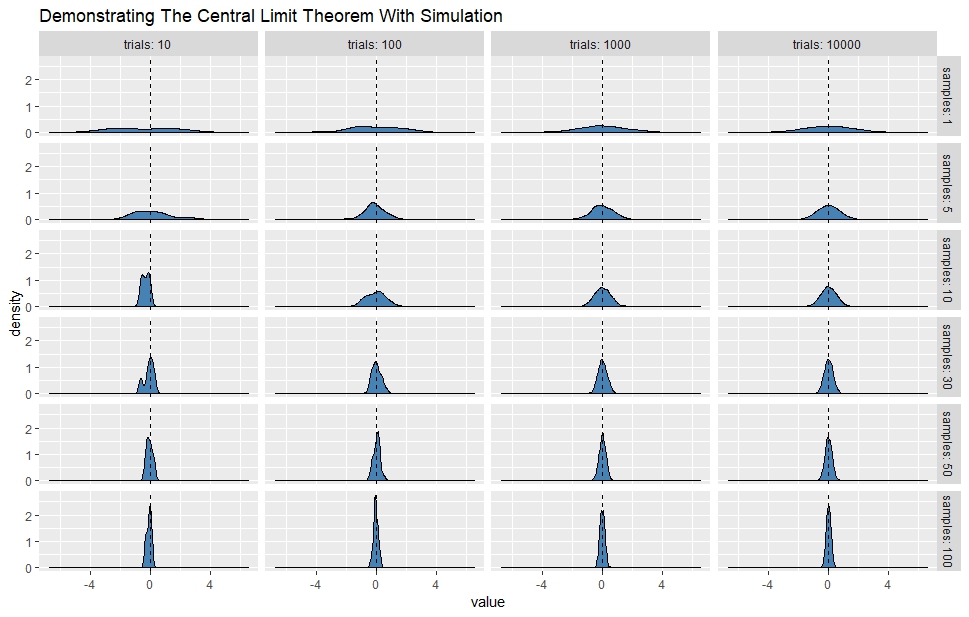
This reminded me of similar criticism, that of frequentism's reliance on the Central Limit Theorem (CLT) presented by Harrell. He gave the argument that the sampling distribution of means from a lognormal population takes a long time to converge, and therefore the CLT is flawed and frequentism is flawed by relying on the CLT. However, if there was a lognormal population, a statistician would make a histogram and observe that it is skewed, and probably consider taking a transformation of the data, such as a log. The critic then says 'ah, but you can't do that' or 'but you don't know what transformation to take'. However, how can the critic even know the population is exactly lognormal to begin with (much like Clayton cannot know a population is exactly Cauchy)? A statistician in real life would simply observe the skew in the sample, apply a transformation, then back-transform to get, for example, a confidence interval on the original non-transformed scale. But the critic would then say 'ah, but now this is an interval on the median, not the mean'. But the frequentist would then say that for skewed distributions like lognormal, they are often described by their median better than their mean, and moreover, equations exist for confidence intervals of their mean and median anyway. The critic would say 'ah, but those equations are difficult'. And on and on and on!
So Bayesians are able to know an underlying F (Cauchy or lognormal) holds exactly, but frequentists aren't. Totally logical and fair.
This also reminded me of the cute critique of:
Assume a male took a test for ovarian cancer with specificity of 99.99%. For H0: no cancer present vs H1: cancer present, the p-value would be .0001. A frequentist would conclude the male has ovarian cancer.
Of course, we don't need statistics for this question. One would find out during an "audit" that the person was male, as well as any other questionable research practices. Why this counterexample prevents the frequentist from knowing the person was male, but presumably allows Bayesians to know that information, or why that is a problem with frequentism and not a problem with the medical test, is beyond me.
Monte Carlo works because of SLLN, and is used in everything from estimating pi to developing atomic bombs. Clayton mentions Markov Chain Monte Carlo (MCMC) and Stan at the end of the book. Sampling from a posterior distribution using MCMC has a frequentist feeling about it though. For example:
- Use a burn-in period? Make coin flips > some small number, since relative frequency is "rough" for a small number of flips.
- Use more iterations? Flip the coin more times, you know it will have a better chance of convergence.
- Use more chains? Flip more coins, multiple evidence of convergence is better evidence than few.
- Starting with a different seed? If it still converges with different seeds, this is like entering a "collective" randomly and still getting the same relative frequency.
In
The Interplay of Bayesian and Frequentist Analysis by Bayarri and Berger, they say
...any MCMC method relies fundamentally on frequentist reasoning to do the computation. An MCMC method generates a sequence of simulated values θ1,θ2,...,θm of an unknown quantity θ, and then relies upon a law of large numbers or ergodic theorem (both frequentist) to assert that... Furthermore, diagnostics for MCMC convergence are almost universally based on frequentist tools.
Bayes Theorem
Clayton provides a lot of examples using Bayes theorem to critique frequentism. However, this is weak criticism because the simple Bayes Theorem, despite the name, is not inherently "Bayesian" as he portrays. It is, in fact, fully in the frequentist statistics domain and is a basic result from the multiplication rule and conditional probability. The equation is P(A|B) = [P(B|A)P(A)]/P(B), where A and B are general events. Where Bayes Theorem becomes "Bayesian" is where the P(A) is a probability distribution for a parameter (a "prior"), and definitely "Bayesian" where the P(A) is based, not on prior experiment or objectivity, but on subjectivity. Moreover, if you are "tallying up historical murder records" (ie. frequencies) to get your base rates or priors, are you doing Bayesian statistics or frequentist statistics?
Clayton's courtroom examples are interesting, but non-conclusive, since he assumes what he calls the Bayesian calculations are correct. We simply don't know. But as mentioned, even what he calls the Bayesian calculations here just use Bayes theorem on simple events, which is in the frequentist domain. It is important to stress that the issue with Clark case wasn't due to frequentism or the transposed conditional fallacy as Clayton suggests. The issues were that Meadow's calculation was based on the assumption that two SIDS deaths in the same family are independent, ignoring factors such as both the Clark babies were boys which make cot death more likely, questionable post-mortem examinations of the children, and other issues. To blame all of that on frequentism is not accurate whatsoever. I'm not even sure any type of probability is the correct tool for the job of legal settings. Regardless, in court settings you need more than logic, you need evidence.
In some cases a frequentist can assign probability to single events using a prediction rule. For example, P(An+1) = xbarn, where it is just a matter of choosing an appropriate statistical model.
Confidence, Likelihood, Probability: Statistical Inference with Confidence Distributions by Schweder and Hjort discusses aleatory and epistemological probability from a frequentist point of view.
Jaynes, Jaynes, and more Jaynes
There are several types of Bayesian groups (usually based on how you get the priors: objective, subjective, empirical). Probably joking a little, Good notes that there are quite a few varieties of Bayesian. Clayton is presumably in the objective camp.
Clayton continues Jaynes' attacking style: "ad hoc", "cookbook", "orthodoxians", "not from first principles", "psychosemantic trap", "loose amalgam", "half-baked", "repackaged", "ruinous", "disease", "boring", "dangerously misleading", "destructive", "irredeemably wrong", "logically bankrupt", "controversial", "hallucinations", "broken", "held together by suggestive naming, catchy slogans, and folk superstition", and etc. See Probability Theory: The Logic of Science by Jaynes.
But putting this bluster aside, the question remains of why is this style of probability and statistics not used the most after all this time if it is as superior as is being claimed? If it has the "unifying principles", the secret sauce if you will, to solve "real scientific problems", why doesn't everyone use it now? Is everyone just ignorant? Or are the frequentist methods just useful?
Cox theorems as Cox wrote them (and as Jaynes repeated) were found later to not be rigorous and have a flaw in which Halpern and others found a counterexample (see A Counterexample to Theorems of Cox and Fine and Cox's Theorem Revisited by Halpern). The theorems have been patched up since, so to speak (see Bridging the intuition gap in Cox's theorem by Clayton). They also have their own "ad hockeries", to use Jaynes' term. For example, the entire issues of priors aside, it relies on classical propositional logic that is not always appropriate.
It is apparent to me that Jaynes overpromised (it takes everything into account automatically!) and underdelivered, and so was somewhat left behind by practitioners. But that certainly doesn't have to be the case. Any Bayesian approach needs to be operationalized, not just developed mathematically or used to attack frequentism. For example, for survey processing, how about creating a frame, taking a sample, imputation or weight adjustment for missing data, outlier detection/removal, estimation and variance estimation, and tests from survey year to year to see if totals are 'significant' (use whatever analogous Bayesian statistic(s) you'd like), in a fully Bayesian treatment. But one requirement is that it has to be "from first principles" as Jaynes liked to say. This is a very common survey setting that frequentist methods can do well even if Jaynes dismisses that very important function as ad hoc. It appears it is Bayesians, not frequentists, who spend their time with toy examples.
Jaynes himself wrote "...Fisher was never able to exhibit a specific problem in which his methods gave a satisfactory result and Jeffreys' methods did not". I would say that is false. Fisher was involved with highly original mathematics for a test of significance and confidence interval (circle/cone) for observations on a sphere in his Dispersion on a Sphere. Fisher solved the statistics questions posed by Runcorn, whose ideas moved us away from "the static, elastic Earth of Jeffreys to a dynamic, convecting planet", as detailed in From polar wander to dynamic planet a tribute to Keith Runcorn. Fisher influencing statistics much more than Jeffreys is evidence enough that Fisher's methods are giving more satisfactory results.
If Jaynes wants frequentists to write freq(X) instead of prob(X), then Bayesians should write belief(X) instead of prob(X).
Eugenics
Here Clayton tries to the link eugenics and genetic interests of Galton, K. Pearson, and Fisher to Nazis, to discredit a frequentist approach. But ask yourself, does P(eugenic interest|Nazi) imply high P(Nazi|eugenic interest)?
Or consider the equally bad argument: Bayes was religious, and if one assigns prior(god exist) large, massage the input data, then one can show posterior(god exist) is large, which was Bayes' goal. Are all believers that were motivated by that logic, and went on to commit atrocities in the name of religion, or who condemn groups of people to hell, Bayesian probability's fault? Of course not.
In fact, in The Reverend Thomas Bayes, FRS: A Biography to Celebrate the Tercentenary of His Birth, we find this quote from Price:
The purpose I mean is, to shew what reason we have for believing that there are in the constitution of things fixt laws according to which events happen, and that, therefore, the frame of the world must be the effect of wisdom and power of an intelligent cause; and thus to confirm the argument taken from final causes for the existence of the Deity.
That is, Price, and maybe Bayes, saw Bayes theorem as a way to provide a "proof" for the existence of God (the one they believed in anyway), and also therefore refuting Hume on miracles.
In any case, saying because Fisher (Jeffries too) were heavy smokers, therefore frequentism (Bayes) is false, is a bad argument.
Clayton also doesn't give the full quote from Fisher. If he had, the quote wouldn't look as bad. Fisher's full quote from The Outstanding Scientist, R.A. Fisher: His Views on Eugenics and Race by Bodmer, Senn, et al is:
As he has been attacked for sympathy towards the Nazi movement, I may say that his reputation stood exceedingly high among human geneticists before we had heard of Adolph [sic] Hitler. It was, I think, his misfortune rather than his fault that racial theory was a part of the Nazi ideology, and that it was therefore of some propaganda importance to the Nazi movement to show that the Party supported work of unquestioned value such as that which von Verschuer was doing. In spite of their prejudices I have no doubt also that the Party sincerely wished to benefit the German racial stock, especially by the elimination of manifest defectives, such as those deficient mentally, and I do not doubt that von Verschuer gave, as I should have done, his support to such a movement. In other respects, however, I imagine his influence was consistently on the side of scientific sanity in the drafting and administration of laws intended to this end.
The article by Bodmer, Senn, et al goes on to say:
These statements have been interpreted by some as suggesting that Fisher referred to elimination in the sense of killing or at least compulsory sterilisation or institutionalisation, and so was a Nazi sympathiser. This is, however, in obvious disagreement with his very clearly stated views that sterilisation should be voluntary and consistent with his support for the Brock report.
In other words, Fisher was a genetics sympathizer, not a Nazi sympathizer. But even if Fisher himself was Hitler, that wouldn't change anything. It is a desperate distraction that literally has nothing to do with the mathematics behind p-values or anything else. Simply stated, analyzing a now socially bad thing using statistical methods does not mean that the statistical methods are flawed or should be avoided by others. And this goes double when you purposefully leave out good things that were/are analyzed by said statistical methods. Fisher doing experimental agricultural research to save millions from starvation through rational crop breeding programs? Neyman was a human rights activist? Don't mention those.
Objectivity
Subjectivity in general isn't any problem. All scientific disciplines use subject matter input, hunches, current scientific knowledge, and so on. But priors are not every type of belief or knowledge. What is meant by "priors" in Bayes is very specific; they are probability distributions on parameters. One could probably argue that Bayesians may want to blur the differences between mathematical priors and background knowledge, to blunt the criticisms against problematic but fundamental Bayesian concepts involving priors.
See for example, Prior Information in Frequentist Research Designs and Social (Non-epistemic) Influences: The Case of Neyman's Sampling Theory by Kubiak and Kawalec, showing that "priors", in the loose sense of background knowledge, are used in frequentism (or any other area of study, I'd imagine). Moreover, Confidence, Likelihood, Probability: Statistical Inference with Confidence Distributions by Schweder and Hjort, notes that instead of updating the prior/posterior distribution, updating can be done on the likelihood.
To compare using Bayesian priors, which are putting possibly brittle subjective probability distributions on parameters to using any inputs for an analysis and saying "well, both are the same thing really" is simply mistaken.
Clearly some objectivity does exist with probability. Likelihoods and data dominate about any priors and beliefs as n increases. Or consider balls cascading down a quincunx or "Galton Board" to form an approximate normal distribution:
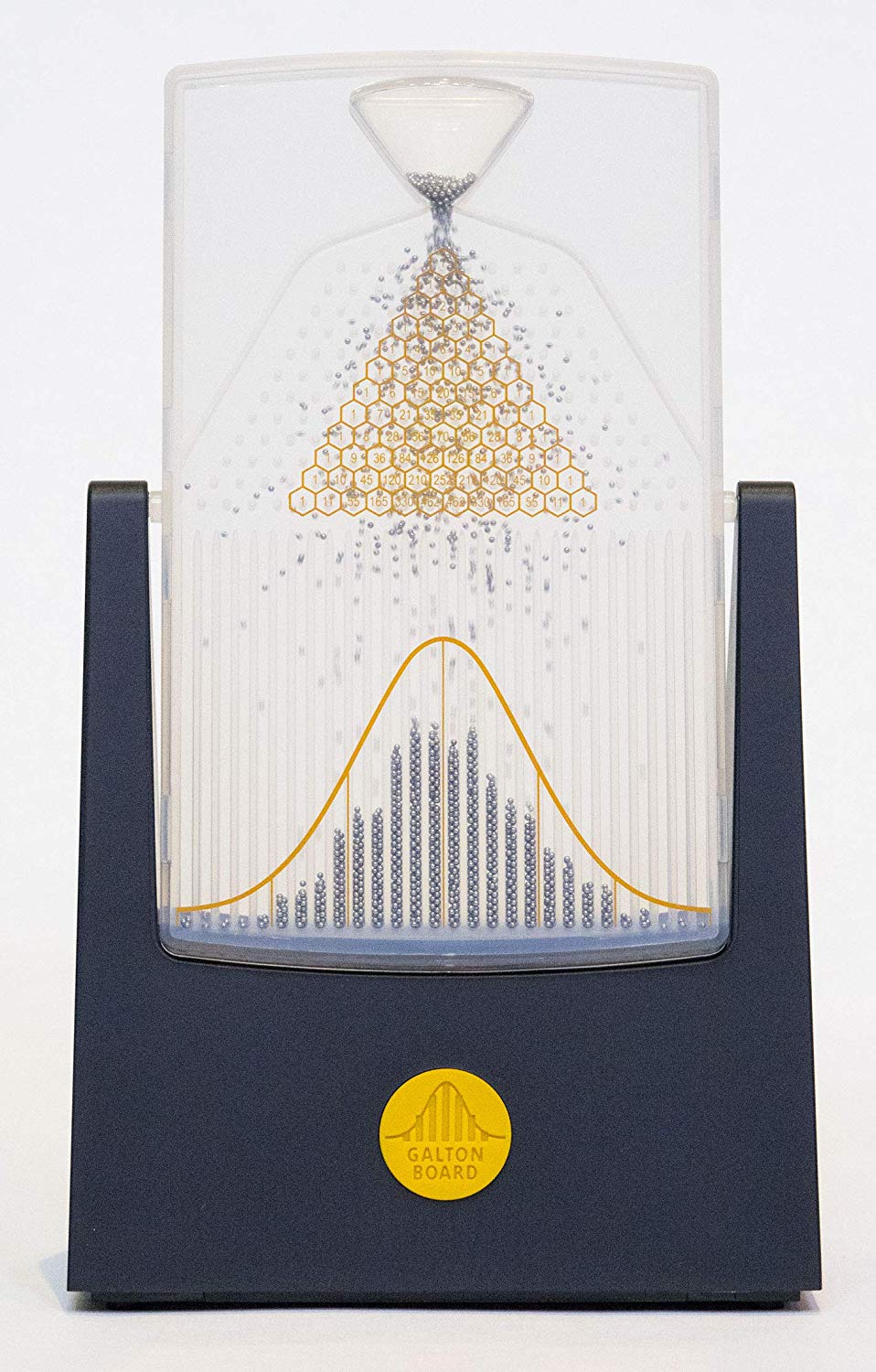
Get yours here, and be sure to check out Four Pines!
Anyone, regardless of beliefs or Bayesian priors, can tip over a Galton board and see the results.
Bad for Science
Clayton would have you believe the big lie that frequentism is bad for science. Surely this is the take-away a reader could get if the author focuses on the misses and not the hits. But let's get out of the book and into reality. See the books The Lady Tasting Tea: How Statistics Revolutionized Science in the Twentieth Century by Salsburg, and Creating Modern Probability: Its Mathematics, Physics and Philosophy in Historical Perspective by von Plato.
Also, see Frequentism is Good response to the "airport fallacy" article by Gunter and Tong that appeared in the 10/2017 issue of Significance, I say:
In my Nobel Prize and Statistical Significance, I show that some current and past Nobel Prize winners and their colleagues use p-values and statistical significance language and concepts in their papers. Note that this is not to say the researchers never use any Bayesian techniques or that they always use p-values and statistical significance. Therefore, these things are not only used in science, but at the highest levels of science.
Also, check out Google's Quantum Supremacy Using a Programmable Superconducting Processor article, specifically the paper it links to and the supplementary information that paper links to. I show in my Quantum Computing and Statistical Significance that there are plenty of examples of p-values, statistical significance, hypothesis testing, sampling, and bootstrapping (ie. all frequentist notions) in their important contribution.
See my Darwin and Statistical Significance. I write about a fairly recent CNN article A PhD student proved one of Darwin's theories of evolution 140 years after his death. The article discusses work by Laura van Holstein on how her work provides evidence for Darwin's unproven hypothesis that a species belonging to a larger genus should also include more subspecies. Here is the journal article by van Holstein and Foley Terrestrial habitats decouple the relationship between species and subspecies diversification in mammals.
Also, please read In Praise of the Null Hypothesis Statistical Test, by Hagen. A sampling of some things he writes
The NHST is not embarrassed by demonstrations that Type I errors can be produced given a large number of replications.
...
The logic of the NHST is elegant, extraordinarily creative, and deeply embedded in our methods of statistical inference.
...
It is unlikely that we will ever be able to divorce ourselves from that logic even if someday we decide that we want to.
...
...the NHST has been misinterpreted and misused for decades. This is our fault, not the fault of NHST. I have tried to point out that the NHST has been unfairly maligned; that it does, indeed, give us useful information; and that the logic underlying statistical significance testing has not yet been successfully challenged.
In Confessions of a p-value lover, Adams, an epidemiologist, dissects popular criticisms of p-values and NHST using a refreshing commonsense approach. Adams writes
They [p-values] have helped me interpret findings, determine which scientific leads to follow-up on, and which results are likely not worth the time and effort.
...
The authors [critics] call for embracing uncertainty, but fail to see that research is done to achieve exactly the opposite: we want to be as informed as possible when making yes/no scientific and policy decisions.
...
While the scaremongering around NHST suggests so, in fact no healthcare policy has ever been based on a mere glance at whether p<0.05.
...
The authors argue that NHST should be banned to solve these problems, except for "specialized" situations - a caveat that will immediately make a careful reader question whether NHST is truly the cause of the problem. If some situations warrant NHST, then clearly NHST should not be blindly banned.
...
Inadvertently, the authors have themselves stumbled upon yet another misuse of p-values and NHST: as a scapegoat for statistical malpractice.
In There is still a place for significance testing in clinical trials, by Cook et al, they say (bolding mine):
The carefully designed clinical trial based on a traditional statistical testing framework has served as the benchmark for many decades. It enjoys broad support in both the academic and policy communities. There is no competing paradigm that has to date achieved such broad support. The proposals for abandoning p-values altogether often suggest adopting the exclusive use of Bayesian methods. For these proposals to be convincing, it is essential their presumed superior attributes be demonstrated without sacrificing the clear merits of the traditional framework. Many of us have dabbled with Bayesian approaches and find them to be useful for certain aspects of clinical trial design and analysis, but still tend to default to the conventional approach notwithstanding its limitations. While attractive in principle, the reality of regularly using Bayesian approaches on important clinical trials has been substantially less appealing - hence their lack of widespread uptake.
...
It is naive to suggest that banning statistical testing and replacing it with greater use of confidence intervals, or Bayesian methods, or whatever, will resolve any of these widespread interpretive problems. Even the more modest proposal of dropping the concept of 'statistical significance' when conducting statistical tests could make things worse. By removing the prespecified significance level, typically 5%, interpretation could become completely arbitrary. It will also not stop data-dredging, selective reporting, or the numerous other ways in which data analytic strategies can result in grossly misleading conclusions.
On the idea of getting rid of frequentist methods, Mayo writes:
Misinterpretations and abuses of tests, warned against by the very founders of the tools, shouldn't be the basis for supplanting them with methods unable or less able to assess, control, and alert us to erroneous interpretations of data
and
Don't throw out the error control baby with the bad statistics bathwater
As far as sample surveys, see U.S. Government Contributions to Probability Sampling and Statistical Analysis for one example. There are sample surveys that have been going on longer than Clayton has been alive.
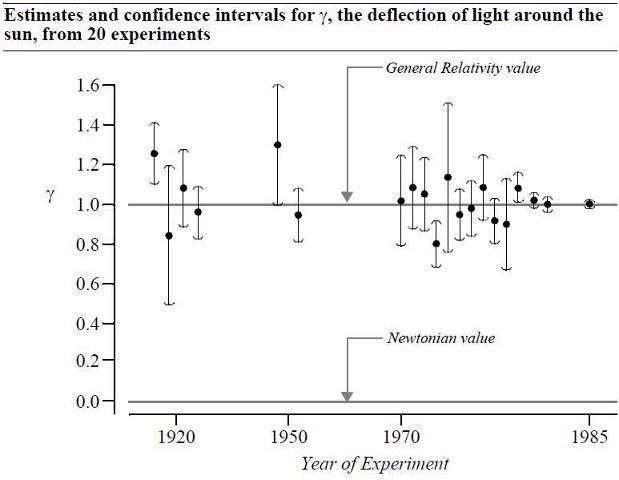
Here is one of my favorite graphs, showing how individual well-designed scientific experiments and confidence intervals can converge over time and improve our understanding of the world.
The evidence continues to strongly reject the critic's hypothesis that p-values and statistical significance are bad for science.
Tell me what I want what I really really want
Variations of the phrase "what we really want is P(H|D)" is something you'll read a lot in this book. This "what we really want to know (or say), is X" has been called "The Statistician's Fallacy" by Lakens. That is, statisticians saying what all researchers supposedly want to know, and not coincidentally the answer X is aligned 100% with the statistician's philosophy of statistics and science!
One could argue the other way, that Bayesians really want to say that their procedures have good long-term performance, good coverage, be free from as much subjectivity as possible, or not be confined to having to try and solve all problems with the same tool.
Let's Make a Deal
The book has a section on the Monty Hall problem. However, the question of "do you switch doors or not?" is also answered handily by several different frequentist approaches. See my The Monty Hall (or Let's Make a Deal) Problem. Notable is that Clayton outright rejects simulation as an answer (apparently choosing valid answers to reject is not ad hoc). In my opinion, it is the most satisfying answer. Of course, in an interview, Clayton talks about how approximations are great and who needs analytic solutions anyway.
Proofs of God
There are proofs of God existing, the resurrection of Jesus, and other miracles, that rely on Bayes theorem. These are silly, but use priors correctly, arguably, especially in the subjective Bayesian paradigm. Some argue that it was Bayes'/Price's intention to use the theorem to refute Hume's argument against miracles. For some examples, see The Probability of God: A Simple Calculation That Proves the Ultimate Truth by Unwin, The Existence of God by Swinburne, and Bayesian evaluation for the likelihood of Christ's resurrection. Are these therefore a mark against Bayesian statistics as a whole? Of course not! So why should misuses or misunderstandings of frequentist statistics or hypothesis testing or p-values count against frequentism?
Can proofs of god(s) type of nonsense occur with misuses of frequentism? Yes, however I would argue that it is more difficult to logically defend that practice in frequentism compared to subjective Bayes in which anyone dream up an equally valid subjective prior for a parameter. In the 1700s, Arbuthnot in his Argument from Divine Providence examined birth records in London from 1629 to 1710. If the null hypothesis of equal number of male and female births is true, the probability of the observed outcome of there being so many male births was 1/282. This first documented use of the nonparametric sign test led Arbuthnot to correctly conclude that the true probability of male and female births were not equal, given the assumptions of the model and the limitations in the data. However, he then took a huge leap, unwarranted by hypothesis testing or science, and attributed that finding to the god he believed in. Let's note that this frequentist proof of god(s) was over 300 years ago, but note that the proofs/disproofs of god(s) using Bayesian probability are not only 300 years ago but are also (shamefully) used in modern times.
Bayes theorem can be seen as a way to avoid changing your strong prior beliefs, since priors equal to 0 or 1 (or even near) would never have a posterior away from 0 or 1, no matter the data observed. Using highly skeptical priors isn't a great solution, because one could claim you're biasing things in the other direction. Also, one can have skeptical priors but also have highly selected data, and then the outcome would erroneously be "blessed" because a skeptical prior was used.
Sherlock Holmes was a Bayesian
Sherlock Holmes was Bayesian! And therefore you should be too. I do not believe Holmes was Bayesian (who cares since he is fictional?), but let's look at some things Holmes said:
- "How often have I said to you that when you have eliminated the impossible, whatever remains, however improbable, must be the truth?", and similar variations
- "We balance probabilities and choose the most likely. It is the scientific use of the imagination."
- "while the individual man is an insoluble puzzle, in the aggregate he becomes a mathematical certainty. You can, for example, never foretell what any one man will do, but you can say with precision what an average number will be up to. Individuals vary, but percentages remain constant. So says the statistician."
- "Data! Data! Data! I can't make bricks without clay."
- "One should always look for a possible alternative, and provide against it."
- "It is certainly ten to one that they go downstream, but we cannot be certain."
- "It's life or death - a hundred chances on death to one on life."
- "Dirty-looking rascals, but I suppose every one has some little immortal spark concealed about him. You would not think it, to look at them. There is no a priori probability about it. A strange enigma is man!"
- Also, in "The Adventures of the Dancing Men", Holmes broke essentially a substitution code using a frequentist solution.
I believe these instances show Holmes using concepts from frequentist, likelihood, and Bayesian schools of thought. And yes, that is my actual tattoo.
Testing ESP
Clayton uses the argument of: studies purport to show evidence for ESP, ESP is bunk, frequentist methods were used, therefore frequentist methods are bunk. Yet, this argument doesn't hold water. If I am hanging a picture and I hit my finger with the hammer, is that the hammer's fault?For starters, if testing claims of ESP, consider lowering α drastically because it is an extraordinary claim that, if true, would change our fundamental knowledge about the world. The James Randi Educational Foundation had a $1,000,000 challenge to anyone demonstrating ESP, psychic, paranormal, etc., powers in a controlled setting, and they took this approach. Suffices to say, using good experimental design and low α precluded winning the money merely by chance. The JREF rightly recognized that setting α should be based on cost of making a Type 1 error.
A Bayesian approach also wouldn't automatically solve the problem. Consider this quote from an ESP study by Jahn: "Bayesian results range from confirmation of the classical analysis to complete refutation, depending on the choice of prior". So how are priors chosen and who choses them?
In any case, obviously attention needs to be paid to practical significance in ESP studies.
9 Problems
I found these problems underwhelming and not really any problem for frequentism. Let's look at them in order, with some thoughts.- base rate neglect
- Bayes theorem with simple events is fully in the frequentist domain
- malfunctioning digital scale
- we will make errors if we "blindly follow" any approach
- extreme data can obviously count as evidence against a hypothesis
- modus tollens and modus tollens probabilized does work
- sure-thing hypothesis
- very contrived example
- "too exhausted" to consider rolling again? Convenient I'd say, because that would clearly be one of the things needed to test the hypothesis.
- problem of optional stopping
- it isn't "only what we got matters" or "what we didn't get but could have got matters", it is "what we got and what we didn't get but could have got matters"
- counterfactual reasoning is essential for science and causal reasoning
- the researchers should get different results even with the same likelihood
- the likelihood principle does not hold in practice with any approach
- optional stopping is issue in Bayesian approaches too
- problem of divided data
- meta analysis
- see severity
- preregistration
- look at practical significance as well as statistical significance. See equivalence testing
- German tank problem
- see Wikipedia's entry on the German tank problem
- frequentism worked there just fine and Bayes did too
- I would say the frequentist solution is easier to do and explain
- testing for independence
- Fisher's exact test works
- many methods for 2x2 tables
- which one a researcher uses depends on assumptions and goals (dismissed as "ad hoc")
- rejecting H0 outright before any analysis since it is continuous and prob(X=x)=0 for continuous X misses the point. The parameter in H0 is in the population and we're seeing "how close" based on the sample
- ditto for "actually independent"
- the lucky experimenter
- can truncate data
- frequentist methods exist that incorporate variable sample size, such as Poisson sampling
- could bootstrap
- finding a lost spinning robot
- median
- equations for approximation exist (difficult, but as palatable as MCMC innards)
- again, solutions dismissed as "ad hoc"
Notable Omissions
Let's look at some things that Clayton did not write about. Most of these things would have strengthened the case for frequentism, but the reader is left unaware. This just goes to show that looking at data that did not occur is important.
Equivalence testing
Equivalence testing is explained in Equivalence Testing for Psychological Research: A Tutorial by Lakens et al. Equivalence testing basically consists of determining the smallest effect size of interest (SESOI) and constructing a confidence interval around a parameter estimate. Using both NHST and equivalence tests might help prevent common misunderstandings of p-values larger than α as absence of a true effect, and of the difference between statistical and practical significance. The researcher sets the smallest effect size of interest (SESOI), and looks not only at statistical significance but also practical significance. Here is a table showing possible outcomes in equivalence testing:
| possible outcome | interpretation |
| reject H0, and fail to reject the null of equivalence | there is probably something, of the size you find meaningful |
| reject H0, and reject the null of equivalence | there is something, but it is not large enough to be meaningful |
| fail to reject H0, and reject the null of equivalence | the effect is smaller than anything you find meaningful |
| fail to reject H0, and fail to reject the null of equivalence | undetermined: you don't have enough data to say there is an effect, and you don't have enough data to say there is a lack of a meaningful effect |
Severity
The notion of "severity" demonstrates frequentism and hypothesis testing and their relation to good science. See Statistical Inference as Severe Testing: How to Get Beyond the Statistics Wars by Mayo, and Severe Testing as a Basic Concept in a Neyman-Pearson Philosophy of Induction by Mayo and Spanos. It essentially formalizes Popper's notion of thoroughly testing a claim. They write:
The intuition behind requiring severity is that:Data x0 in test T provide good evidence for inferring H (just) to the extent that H passes severely with x0, i.e., to the extent that H would (very probably) not have survived the test so well were H false.
Confidence distributions
While Clayton does mention Fisher's failure of fiducial probability in passing, he seems ignorant of its modern development. It seems that fiducial probability was a success for simple cases but possibly not well-defined in more general settings. Confidence distributions (CD) are distribution functions that can represent confidence intervals of all levels for parameters of interest. CDs are extremely fruitful, enabling us to solve all sorts of statistical problems in prediction, testing, simulation and meta analysis, and quite possibly even providing a unifying framework for Bayesian, likelihood, fiducial, and frequentist schools. Far from being a failure, Fisher (again) seems to have paved the way with his work on fiducial probability. See Confidence, Likelihood, Probability: Statistical Inference with Confidence Distributions by Schweder and Hjort.
Efron (Statistical Science, 1998) has said:
"... here is a safe prediction for the 21st century: ...I believe there is a good chance that...something like fiducial inference will play an important role... Maybe Fisher's biggest blunder will become a big hit in the 21st century!"
Fraser (2011) has also said that Bayesian posterior distributions are just quick and dirty confidence distributions.
American Statistical Association's position
Clayton references the ASA's 2016 writing recommending to not rely only on p-values, and their 2019 updating. However, ASA has a more recent document, clarifying their stance. I don't hold this against Clayton, as it came out probably after his book was already complete. To summarize:
- ASA statement on p-values (2016)
- Statistical Inference in the 21st Century: A World Beyond p < 0.05 (2019)
- The ASA President’s Task Force Statement on Statistical Significance and Replicability (2021)
In 1), we learn not to rely only on a single statistic. Hopefully no one was doing that anyway. In 2), we read don't do this and use these statistics instead, yet no cons are discussed about the other statistics. This caused confusion because it was interpreted like "ASA said not to...". Regarding the ~850 signatories from Nature's hit piece, let's try and determine for what value of X, where X is the number of signatories, is it impressive? If only we had some way to say if such an X was significant... And what about the number Y of those scientists all over the world that favor significance testing? I'd opine that Y>>X. With 2), ASA jumped the statistical shark. In 3), we learn p-values are fine and allowed again. Phew.
See The practical alternative to the p-value is the correctly used p-value by Lakens.
Clayton quotes Ioannidis' work a lot on estimates of the number of false positives. However, in his recent Retiring statistical significance would give bias a free pass, he wrote:
Statistical significance sets a convenient obstacle to unfounded claims. In my view, removing the obstacle could promote bias. Irrefutable nonsense would rule.
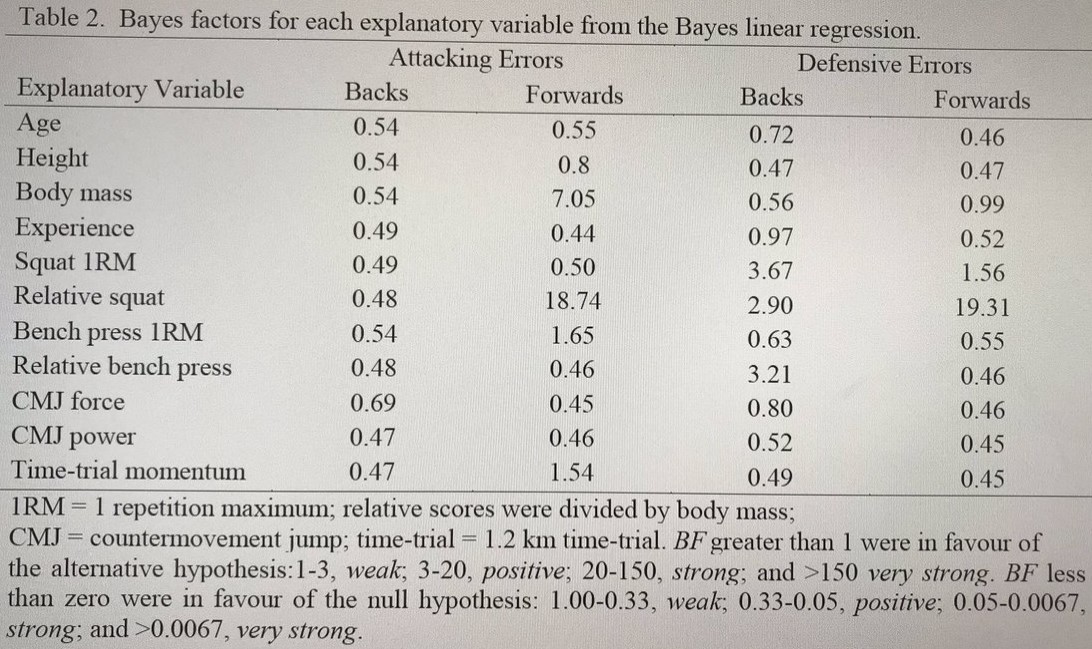
Also see In defense of P values by Murtaugh. The p-value, CI, AIC, BIC, BF, are all very much related. I think about a p-value as a test statistic put on a different scale. Saying a p-value is "bad" is like saying use Fahrenheit (F) over Celsius (C) because C is bad. As an example, consider that the world starts using Bayes Factors (BF) instead of p-values. A question naturally arises, for what values of BF do things become something like "statistically significant"?
Consider the very approximate correspondence between p-values and BFs:
p-value |
Corresponding Bayes Factor |
.05 |
3 - 5 |
.01 |
12 - 20 |
.005 |
25 - 50 |
.001 |
100 - 200 |
Perhaps there would be academic journals that would not let one publish if the BF is not greater than 5. Maybe there would be replications of studies that had large BF that now have a smaller BF. There would probably be plenty of papers saying we need reform because of the misunderstanding of BF even among professional statisticians, or that some other statistic or approach is better than BF. A few people would mention that the first users of BF pointed out these stumbling blocks on misuses of BF a long time ago. One sees the point I hope. Statisticians also use tables, graphs, and other statistics to make conclusions, so an over-emphasis on p-values, BF, etc., is somewhat misguided.
Of course, a rescaled distance of what you observe from what you expect under a model can never be controversial. That's a little like saying if you have a fair coin and do 100 flips, you expect 50 but observe 77. So let's ban the number 27 (=77-50).
Update on BASP
Clayton mentioned the ban on p-values and statistical significance testing in Basic and Applied Social Psychology (BASP) in 2015, but what were the effects after the ban? Did science improve? Ricker et al in Assessing the Statistical Analyses Used in Basic and Applied Social Psychology After Their p-Value Ban write:
In this article, we assess the 31 articles published in Basic and Applied Social Psychology (BASP) in 2016, which is one full year after the BASP editors banned the use of inferential statistics.... We found multiple instances of authors overstating conclusions beyond what the data would support if statistical significance had been considered. Readers would be largely unable to recognize this because the necessary information to do so was not readily available.
Also, please read So you banned p-values, how's that working out for you? by Lakens.
What will happen with those that (claim to) refuse to use p-values in papers, is that they will most likely use p-values behind the scenes to assess the distance between what is observed and what is expected under the model. If they use some alternative, the onus is on them to show it works and to discuss any limitations of the alternative.
Additionally, Trustworthiness of statistical inference by Hand, notes problems with the BASP proposal to ban null hypothesis significance testing.
Stopping
Regarding claiming that Bayesians can stop whenever, just because one can doesn't mean one should. In Stopping rules matter to Bayesians too, Steele writes:If a drug company presents some results to us - "a sample of n patients showed that drug X was more effective than drug Y" - and this sample could i) have had size n fixed in advance, or ii) been generated via an optional stopping test that was 'stacked' in favour of accepting drug X as more effective - do we care which of these was the case? Do we think it is relevant to ask the drug company what sort of test they performed when making our final assessment of the hypotheses? If the answer to this question is 'yes', then the Bayesian approach seems to be wrong-headed or at least deficient in some way.
Also, see Why optional stopping is a problem for Bayesians, by Heide and Grunwald.
Modus tollens
Clayton briefly discusses modus tollens (MT) logic, but only briefly. MT is essentially argument by counterfactual/contradiction/falsification. The logic of modus tollens says P->Q, and if we observe not Q, therefore we conclude not P. Note that P is the null hypothesis H0, and Q is what we'd expect the test statistic T to be under H0. A concrete example is, we agree on assuming a fair coin model. We therefore expect about 50 heads if we flip a coin 100 times. However, we observe 96 heads (96 put on a p-value scale would be an extremely small p-value). Say we also repeat this experiment 3 times and observe 92, 95, and 89 heads. Therefore, we conclude the fair coin model is not good. This type of logical argument is valid and essential for falsification and good science a la Popper. Anticipating the question, yes, MT reasoning is still valid when put in probability terms. Modus tollens, and modus ponens, put in terms of probability effectively introduce bounds, much like in linear programming. See Boole's Logic and Probability by Hailperin, and Modus Tollens Probabilized by Wagner. And simply put, statistical tests "make room" for errors. No one is claiming H0 is true or false in some universal sense, only that evidence for/against H0 with this data, α, β, sample size, experimental design, etc. has been provided.
Dichotomania
Categories are a natural and fine way of observing and learning about the world. One way of understanding why is from An Investigation of the Laws of Thought by Boole. He wrote that X2=X, or X(1-X)=0, where X is a set and the operations are set operations, is the fundamental "law of thought". That is, something cannot be in both sets X and 1-X at the same time. Boole used this law to compute probabilities and statistics. Boole's work was modernized and made rigorous by Hailperin in Boole's Logic and Probability: Critical Exposition from the Standpoint of Contemporary Algebra, Logic and Probability Theory in a linear programming context. Also check out The Last Challenge Problem: George Boole's Theory of Probability by Miller.
Also, Neyman wrote that a:
region of doubt may be obtained by a further subdivision of the region of acceptance
indicating that we can do more than just reject and fail to reject quite easily and naturally if we choose to.
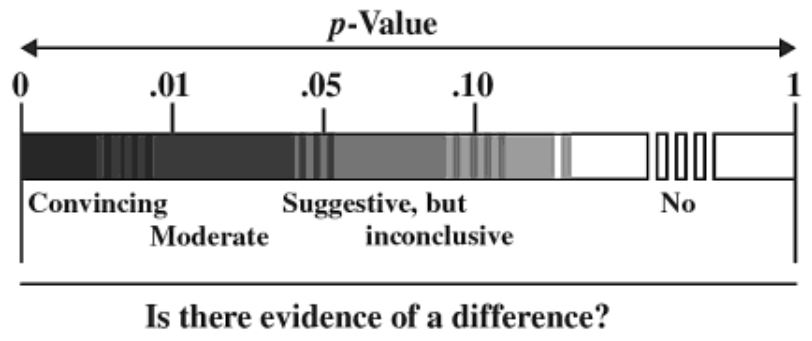
P-values can also be simply reported as-is, as well as interpreted using a spectrum (which of course depends on α too). Consider the following p-value graphic from The Statistical Sleuth: A Course in Methods of Data Analysis:
Also, consider the following Bayes factor range interpretations from a study:
The Bayes factors could also be interpreted just using a strong/weak dichotomy if a researcher wanted to.
Reference class problem
A reference class problem (which is not really a problem) exists with not just frequentism, but also Bayesian and all other interpretations of probability. For example, does the prior you're using on the ability of soccer players apply for all players, all male players, all players within a given year, all players on a given team, etc. No matter the measure, we always need to define what it is a measure of. Fisher himself pointed this out in the 1930s and Venn 70 years before that (and Fisher notes that about Venn)! Just like all probabilities are conditional, we all belong to different classes and frequency(male) is different from frequency(male wears glasses), etc. This is why the context of the problem is important where you define all of these things. Often if a class is too small or empty, and could not meet distributional assumptions, one can "collapse" to the next class that is not too small or empty. As an example, consider the North American Industry Classification System, or NAICS, levels. For example, if there were few or no observations in NAICS 11116 "Rice Farming" you could collapse to NAICS 1111 "Oilseed and Grain Farming". If there were few or no observations in NAICS 1111, you could collapse to NAICS 111 "Crop Production". And last, if there were few or no observations in NAICS 111, you could collapse to NAICS 11 "Agriculture, Forestry, fishing and Hunting". A scenario like this could come into play if setting up cells for imputation, for example.
Likelihood principle
A common claim is that frequentism violates the Strong Likelihood Principle and therefore frequentism is wrong. However, the likelihood itself doesn't obey probability rules, needs to be calibrated, doesn't have as high of status as probability, and is merely comparative (ie. H0 relative to H1) rather than corroborating (ie. evidence for an H), so using the likelihood alone is not a reasonable way to do science. See In All Likelihood: Statistical Modelling and Inference Using Likelihood by Pawitan.
Additionally, the SLP violation charge has also been severely critiqued and found wanting. If the Weak Conditionality Principle is WCP, and the Sufficiency Principle is SP, in On the Birnbaum Argument for the Strong Likelihood Principle by Mayo, she writes:
Although his [Birnbaum] argument purports that [(WCP and SP) entails SLP], we show how data may violate the SLP while holding both the WCP and SP.
Also see Flat Priors in Flatland: Stone's Paradox by Wasserman discussing Stone's Paradox. Wasserman says:
Another consequence of Stone's example is that, in my opinion, it shows that the Likelihood Principle is bogus. According to the likelihood principle, the observed likelihood function contains all the useful information in the data. In this example, the likelihood does not distinguish the four possible parameter values. But the direction of the string from the current position - which does not affect the likelihood - clearly has lots of information.
In short, the likelihood principle says that if the data are the same in both cases, the inferences drawn about the value of a parameter should also be the same. The Bayesian and likelihood approaches may view the likelihood principle as a law, but frequentists understand it is not one. Consider the specific examples of having the same data where the inferences are completely different, as they should be. The examples are not paradoxes, but demonstrate that the experimental design, sampling distribution, and test statistic (ie. taking all evidence into consideration) are of utmost importance in making sound inference. The confidence distributions in these examples (and p-values) would be different. See Confidence, Likelihood, Probability: Statistical Inference with Confidence Distributions by Schweder and Hjort, showing an example of this.
Additionally, the likelihood principle is violated in Bayesian posterior predictive checking.
Priors
Almost nothing was mentioned on how priors are actually developed (nor problems with higher dimensions). How are readers and practitioners supposed to digest what amounts to just-think-about-it-like-any-rational-person-would type of advice? Priors are always assumed to be right or at least defendable.
Gelman has noted that:
Bayesians have sometimes taken the position that their models should not be externally questioned because they represent subjective belief or personal probability. The problem with this view is that, if you could in general express your knowledge in a subjective prior, you wouldn't need formal Bayesian statistics at all: you could just look at your data and write your subjective posterior distribution.
Also, Mayo details that Gelman has made the remark that a Bayesian wants everybody else to be a non-Bayesian That way, he wouldn't have to divide out others' priors before he does his own Bayesian analysis.
It is often true that as n/N goes to 1, or as n gets large, the likelihood tends to dominate the prior. As the likelihood dominates the prior, that is equivalent to your beliefs mattering less and less. Also, hypothesis tests can serve to reject priors.
It is also known that Bayesian priors can be "brittle". See On the Brittleness of Bayesian Inference and Qualitative Robustness in Bayesian Inference by Owhadi, Scovel, and Sullivan.
Additionally, a Bayesian approach can suffer from false confidence. Balch, Martin, and Ferson in their Satellite Conjunction Analysis and the False Confidence Theorem, discuss that there are:
probabilistic representations of statistical inference, in which there are propositions that will consistently be assigned a high degree of belief, regardless of whether or not they are true.
In their work, using those modes of statistical inference could result in probability dilution and false confidence, that is, a severe underestimate of satellite collision risk exposure, or a high confidence that their satellites are safe whether or not they really are safe. This occurs regardless of the validity of the mathematics. In other words, it is more a mismatch between the mathematics of probability theory and the uncertainty or subject matter to which it is applied. The false confidence theorem shows that all epistemic probability distributions (which includes Bayesian) suffer from arbitrarily severe false confidence.
Thus, our goal has been to help satellite operators identify tools adequate for limiting the literal frequency with which collisions involving operational satellites occur. Framing the problem in frequentist terms enables us to do that, whereas framing the problem in Bayesian terms would not.
Interestingly, the size of the false confidence can "only be found for a specific proposition of interest through an interrogation of the belief assignments that will be made to it over repeated draws of the data". That is, frequentist confidence intervals and regions do not suffer from false confidence.
Also, check out An exposition of the false confidence theorem by Carmichael and Williams.
In A Systematic Review of Bayesian Articles in Psychology: The Last 25 Years by van de Schoot et al, the popularity of Bayesian analysis has increased since 1990 in psychology articles. However, quantity is not necessarily quality, and they write:
"...31.1% of the articles did not even discuss the priors implemented"
...
"Another 24% of the articles discussed the prior superficially, but did not provide enough information to reproduce the prior settings..."
...
"The discussion about the level of informativeness of the prior varied article-by-article and was only reported in 56.4% of the articles. It appears that definitions categorizing "informative," "mildly/weakly informative," and "noninformative" priors is not a settled issue."
...
"Some level of informative priors was used in 26.7% of the empirical articles. For these articles we feel it is important to report on the source of where the prior information came from. Therefore, it is striking that 34.1% of these articles did not report any information about the source of the prior."
...
"Based on the wording used by the original authors of the articles, as reported above 30 empirical regression-based articles used an informative prior. Of those, 12 (40%) reported a sensitivity analysis; only three of these articles fully described the sensitivity analysis in their articles (see, e.g., Gajewski et al., 2012; Matzke et al., 2015). Out of the 64 articles that used uninformative priors, 12 (18.8%) articles reported a sensitivity analysis. Of the 73 articles that did not specify the informativeness of their priors, three (4.1%) articles reported that they performed a sensitivity analysis, although none fully described it."
These practices are very worrying.
Every Bayesian analysis requires a sensitivity analysis on priors.
Only sampling error?
Clayton claims that frequentism only considers sampling error. This is a very common misconception held by critics of frequentism. The total survey error approach in survey statistics, for example, focuses on many types of errors, not just sampling error. In the 1940s, Deming discussed many types of non-sampling errors in his classic Some Theory of Sampling. Also see Total Survey Error in Practice by Biemer, Leeuw, et al. It is also very necessary to mention Pierre Gy's theory of sampling. Gy developed a total error approach for sampling solids, liquids, and gases, which is very different from survey sampling. See A Primer for Sampling Solids, Liquids, and Gases: Based on the Seven Sampling Errors of Pierre Gy by Patricia Smith. Statisticians do their best to minimize sampling and non-sampling errors.
This is similar to critics believing that frequentism is NHST. Of course, frequentism is also very concerned with survey and experimental design.
If there was a Bernoulli's fallacy, then sampling wouldn't work so well as it does, and we would not learn about a population parameter as we take samples and calculate statistics, assuming our samples are well-designed. In fact, as sample size / population size, or n/N, approaches 1, we have sampled the entire population (i.e., taken a census), and learned about the population exactly, barring any non-sampling errors of course. Just the fact that sampling works so well is evidence there is no Bernoulli fallacy.
Bayesian QRPs
Clayton seems to believe that no QRPs with Bayes can possibly exist, because he doesn't mention any with any detail. This is beyond naive.
While Bayesian inference avoids the typical problems of frequentist inference with NHST, it is not exempt from limitations. These include misinterpretation of Bayes factors, mindless use of "objective" or "default" priors (e.g., exclusive reliance on fat-tailed Cauchy priors in statistical packages), bias in favor of the null hypothesis, and potential mismatch between inference with Bayes factors and estimation based on the posterior distribution, subjectivity, ignoring stopping, brittle priors, false confidence, prior hacking, not reporting sensitivity analysis, etc.
Elise Gould has said:
Non-NHST research is just as susceptible to QRPs as NHST.
The loudest claims of frequentism used to "p-hack" may really just be "p-envy", or perhaps what Wasserman calls "frequentist pursuit". If anything, Bayesian inferences can increase these problems, or create a different set of problems, because in addition to the usual myriad of things to choose from in any analysis, now we have an infinite number of priors and other statistics we can choose from. See Degrees of Freedom in Planning, Running, Analyzing, and Reporting Psychological Studies: A Checklist to Avoid p-Hacking by Wicherts, Veldkamp, et al, for a good discussion of p-hacking. Also, make sure not to look at data prior to making the prior, and don't retry your analysis with different priors. Of course, any method, frequentist or Bayesian (or anything else), can be "hacked" or "gamed". The article Possible Solution to Publication Bias Through Bayesian Statistics, Including Proper Null Hypothesis Testing by Konijn et al discusses "BF-hacking" in Bayesian analysis, and notes
"God would love a Bayes Factor of 3.01 nearly as much as a BF of 2.99."
Tests for nonrandomness
Tests for nonrandomness are very important types of tests in frequentist statistics. Such tests are intimately related with testing pseudorandom number generators (PRNGs), which are incredibly important. An example of just one test, is a nonparametric test for nonrandomness, from I believe the 1930s-1950s, called the Runs Test. It tests the hypotheses:
H0: sequence is random
H1: there are runs present (ie. sequence is nonrandom)
Lets say a computer node has states Up and Down and we're getting state updates every so many minutes. Reading from left to right, oldest state event to newest, we have:
A node that isn't "flapping":
[1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1] ...
And at some point starts flapping:
[0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1] ...
And then starts settling down to a constant state:
[1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1] ...
One simply has to count the number of 0s, n0, the number of 1s, n1, and the number of runs, R. A run is simply the number of groups of 0s and 1s. For example, the three sequences above have 3, 12, and 11 runs.
We also need the expected number of runs, E(R), and the expected standard deviation of runs, Std(R).
E(R) = ((2*n0*n1)/(n0+n1))+1
Std(R) = ((2*n0*n1*(2*n0*n1-n0-n1))/((n0+n1)2*(n0+n1-1)))0.5
Ideally, we'd want at least 25 observations to use the normal distribution. You want this for two reasons. The first reason is that your probability statements will be better. The second reason is that working with the discrete distribution is really, really nasty for this particular problem even if that would get you exact probability statements.
Converting into a Z-score, we get Zobs = (|R-E(R)|-.5)/Std(R), because we are making a "continuity correction". Then you'd conclude there are runs of the 10101010101010 "flapping node" variety for large values of Zobs. Specifically, you'd compare Zobs to Zalpha/2, where alpha = P(concluding flapping nodes are present|flapping nodes are not present), ie. making an error.
What if you have more than 2 states, for example, Up, Warning, Down? There is a "k-category extension" of the runs test that handles these situations. The only things that would change are the equations for the expected number of runs, E(R), and the expected standard deviation of runs, Std(R). All of the other logic would be the same. Here are E(R) and Std(R) for the k-category extension of the runs test:
E(R) = [ n*(n+1)-sum(ni2, i=1 to k) ] / n
Std(R) = ( [ sum(ni2, i=1 to k)*(sum(ni2, i=1 to k) + n(n+1)) - 2n*sum(ni3, i=1 to k) - n3 ] / (n2*(n-1)) ).5
Please check out the great book Nonparametric Statistical Inference, by Gibbons and Chakraborti, for the theory on the runs test and many, many more nonparametric statistics topics. Another fantastic book on nonparametric statistics (even has some Bayesian methods in there) is Nonparametric Statistical Methods by Hollander, Wolfe, and Chicken.
Origins of α = .05
Fisher noted well before critics that:
It is open to the experimenter to be more or less exacting in respect of the smallness of the probability he would require before he would be willing to admit that his observations have demonstrated a positive result. It is obvious that an experiment would be useless of which no possible result would satisfy him.
See his Statistical Methods, Experimental Design, and Scientific Inference
Note that "arbitrary" does not mean there is no reasoning at all behind using α = .05. Fisher basically said it was convenient, and resulted in a z-score of about 2, and made tables in his books (pre-computer times) easier. More importantly, the use, as Fisher knew and wrote about, roughly corresponded to previous scientific conventions of using probable error (PE) instead of standard deviation (SD). The PE is the deviation from both sides of the central tendency (say a mean) such that 50% of the observations are in that range. Galton wrote about Q, the semi-interquartile range, defined as (Q3-Q1)/2, which is PE, where Q3 is the 75th percentile and Q1 is the 25th percentile. For a normal distribution, PE ~ (2/3)*SD. Written another way, 3PE ~ 2SD (or a z-score of 2). The notion of observations being 3PE away from the mean as very improbable and hence "statistically significant" was essentially used by De Moivre, Quetelet, Galton, Karl Pearson, Gosset, Fisher, and others, and represents experience from statisticians and scientists. See On the Origins of the .05 Level of Statistical Significance by Cowles and Davis.
Setting α does not have to be totally arbitrary, however. α is the probability of making a Type 1 error, and should be set based on the cost of making a Type 1 error for your study, as well as perhaps based on the sample size in your study, and adjustments for multiple testing. For example, in "The Significance of Statistical Significance", Hal Switkay suggests roughly setting α based on 1/sample size. Any cutoff, such as cutoffs for determining "significant" Bayes factors, if not set with some reasoning, can also run into the same charge of being arbitrary.
Moreover, there is ample evidence to show that using α=.05 has lead to good science. For example, see When the Alpha is the Omega: P-Values, 'Substantial Evidence,' and the 0.05 Standard at FDA, by Kennedy-Shaffer.
What I'd like to know is, why the "it is arbitrary!" criticism doesn't apply to the Bayesian 1/3<BF10<3 for denoting inconclusive or weak evidence (or 1/a<BF10<a to be general).
Kolmogorov
Clayton mentions that nowhere in Kolmogorov's mathematical axioms is a frequency interpretation mentioned. Of course, other critics have mentioned his theorems have too much frequentist baggage.In any case, when going from the mathematical to the real world, which is arguably a more important world, Kolmogorov himself noted in his On Tables of Random Numbers the contribution of von Mises
"...the basis for the applicability of the results of the mathematical theory of probability to real 'random phenomena' must depend on some form of the frequency concept of probability, the unavoidable nature of which has been established by von Mises in a spirited manner."
As well as in his Foundations of the Theory of Probability
"In establishing the premises necessary for the applicability of the theory of probability to the world of actual events, the author has used, in large measure, the work of R. v. Mises"
And more...
The book also does not mention in any real detail the many positive contributions of frequentism to: sequential analysis, jackknife, bootstrap, survey sampling, quality control, meta analysis, permutation tests, adaptive tests, nonparametric statistics, machine learning, and model checking.
Clayton's Fallacy
Instead of "Bernoulli's Fallacy", here are some examples of what could comprise "Clayton's Fallacy":
- claiming frequentists only focus on sample probabilities
- claiming frequentists rely fundamentally on WLLN
- claiming frequentists confuse P(D|H) with P(H|D) (the probabilistic version of the transposed conditional fallacy)
- claiming P(H|D) = P(H|D, beliefs) or P(H|D) = Belief(H|D) (i.e. saying "probability" is the same as "belief" or "chance" or "uncertainty")
- claiming Prior(effectiveness of frequentism) or Posterior(effectiveness of frequentism) are small considering its positive uses in the world
- claiming to know a true underlying F which nobody really knows
- confusing a mathematical world with the real world
- pretending QRPs cannot possibly happen with Bayesian probability/statistics
Conclusion
You can be coherent with probability, but keep in mind this means you can be coherently wrong. Trying to position Bayesian probability/statistics as "wokeistics" is not a good look, and neither is bragging that you use the same tool for every task. Saying frequentism is bad for science, saying Pearson and Fisher were Nazis, etc., is what I would call "proba(bility)ganda". The success of survey sampling, quality control, experimental design, equivalence testing, and much more, shows frequentism is not flawed as suggested when doing probability/statistics in the real world. There is unifying logic in a frequentist approach, that of sampling and being flexible, which critics attempt to dismiss entirely and negatively as "ad hoc". Using preregistration, improving experimental design, allocating budget toward repeating experiments, and ignoring arbitrary journal publishing requirements, seem like sensible ways to proceed for everyone.
Despite my criticisms of its unconvincing criticisms on frequentism, I recommend this book. Clayton is an excellent writer and expositor in general. I recommend his YouTube channel videos where he explains content from Probability Theory: The Logic of Science, by Jaynes. Despite my disagreement with the contents of this book, I would look forward to buying Clayton's future books.
I also do recommend Bayesian probability/statistics depending on the situation ("ad hoc" I know!). If it is a small sample situation, if strong modelling assumptions are needed, for comparisons to frequentist hypothesis testing, missing data situations, multiple imputation, small area estimation, and empirical Bayes, are all some examples of where I have used Bayesian methods. Additionally, one can evaluate any Bayesian method based on their frequentist performance.
Thanks for reading.
Please anonymously VOTE on the content you have just read:
Like:Dislike: