Email news@statisticool.com to sign up to receive news and updates
Tiling a Square
6/12/16
Say you have a large image that you need rendered. It might be advantageous to you to split up that image and have each "tile" rendered on a different machine. Afterwards, you'd just have to stitch the parts back together. I recently helped my brother with the math for this.
Here is an example of a large image with one tile:
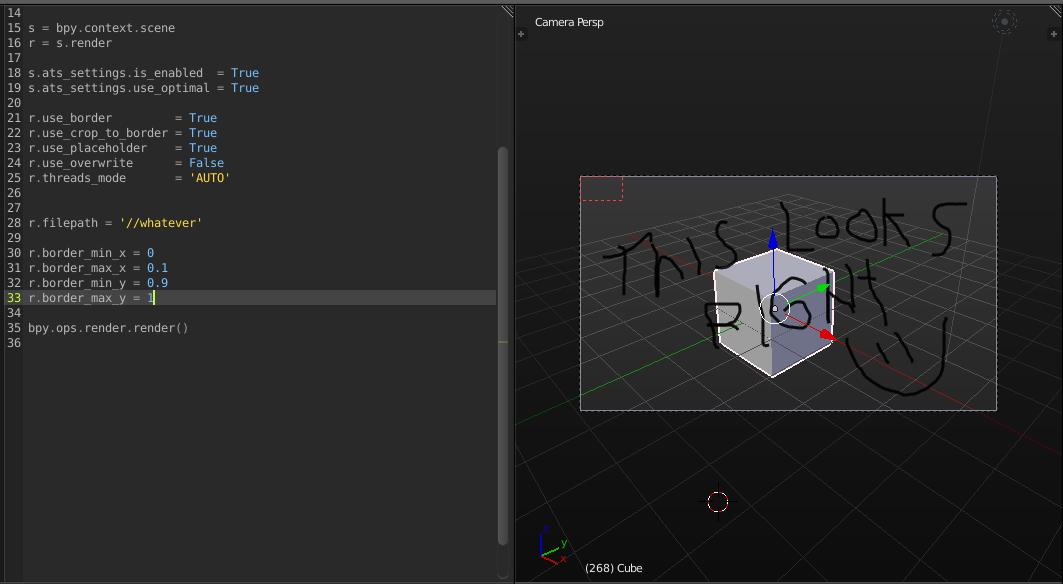
I simpilifed the problem by assuming that the original image is a large square. We will be tiling this square by using m squares.
One interesting twist with this problem, is that the Blender program needs the "window" for each tile. So it isn't a matter of converting coordinates to new coordinates, but converting (i,j), where i is rows and j is columns, to xmin, xmax, ymin, and ymax, where these x and y min's and max's define a tile's window.
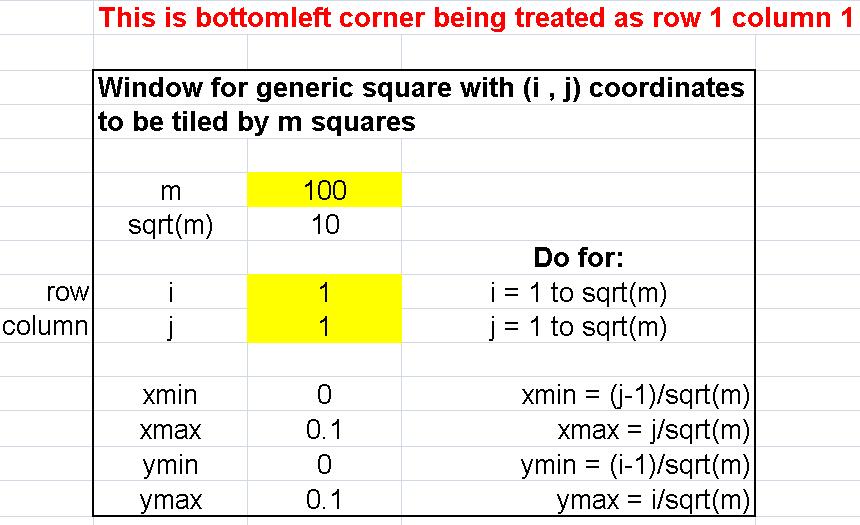
I recognized that if we have a square, and we're using m squares to tile, then m needs to be a square number. For example, 4, 16, 25, 36, etc. For example, if we use m = 100 squares, then we'll have a 10x10 grid that will tile the original square. Note that sqrt(100) = 10.
Therefore, to calculate the windows, we will go from i = 1 to sqrt(m) and j = 1 to sqrt(m) and calculate
- xmin = (j-1)/sqrt(m)
- xmax = j/sqrt(m)
- ymin = (i-1)/sqrt(m)
- ymax = i/sqrt(m)
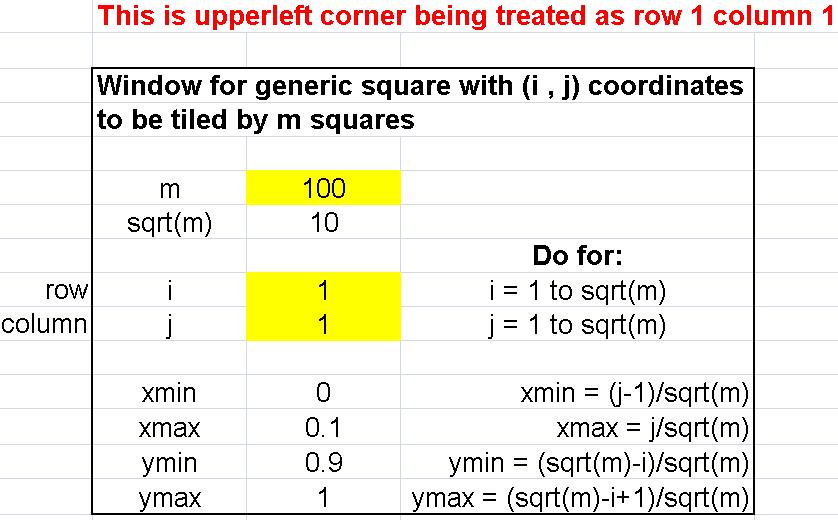
Another requirement, however, was that the Blender program needs the upperleft corner of the square treated as row 1 column 1. The standard math way, however, is treating the lowerleft corner as row 1 column 1, so I needed to change how the window was calculated.
Therefore, to calculate the windows, we will go from i = 1 to sqrt(m) and j = 1 to sqrt(m) and now calculate
- xmin = (j-1)/sqrt(m)
- xmax = j/sqrt(m)
- ymin = (sqrt(m)-i)/sqrt(m)
- ymax = (sqrt(m)-i+1)/sqrt(m)
This was an interesting application of some basic math and I enjoyed it very much. Thank you for reading this.
Please anonymously VOTE on the content you have just read:
Like:Dislike:
If you enjoyed any of my content, please consider supporting it in a variety of ways:
- PLEASE take a moment to check out two GoFundMe fundraisers I set up. The idea is to make it possible for me to pursue my passions. My goal is to be able to create free randomized educational worksheets and create poetry on a full-time basis. THANK YOU for your support!
- Email news@statisticool.com to sign up to receive news and updates
- Donate any amount via PayPal
- Take my Five Poem Challenge
- Subscribe to my YouTube channel
- Visit my Amazon author page
- Buy what you need on Amazon using my affiliate link
- Follow me on Twitter here
- Buy ad space on Statisticool.com
AFFILIATE LINK DISCLOSURE: Some links included on this page may be affiliate links. If you purchase a product or service with the affiliate link provided I may receive a small commission (at no additional charge to you). Thank you for the support!