Pizza Math

4/12/05

I've always believed that a good way to teach mathematics is to play with your food. Food is something that is often around, is easy to work with, and comes in many colors, shapes, and sizes. The only drawback that I can think of, is that the dog really can eat your homework.

This informal article will discuss a food math problem involving pizza. The situation described actually occurred.

Slicing a pizza fairly

Imagine you're dining with your best friend and you get to that last slice of pizza. Your friend is still hungry, and since you're in a sharing mood, you decide to split it, fairly, with your best friend. Where do you slice the pizza in order to make the slices equal?

Let's model our pizza as an isosceles triangle with height h and base with length b. You have measured h and b.

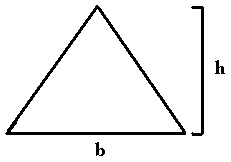
Simple! Just cut the pizza at b/2 to get two equal slices.

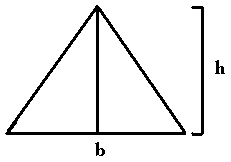
This is called the Vertical Cut. However, you know your friend dislikes the crust, doesn't want to have anything to do with it, and wants you to have the crust. That is great news because you absolutely love the crust! You can't just cut crust off because then the slices wouldn't be equal in size. You must make a Horizontal Cut, so that you get the bottom slice with the crust, your friend gets the top slice with no crust, and yet the slices have equal areas.

How high up do we make the cut? Say we make it x high. This leaves h-x height above the cut, and splits the original slice of pizza, a large isosceles triangle, into a smaller isosceles triangle with height h-x and base d, and an isosceles trapezoid, with height x and base lengths of b and d.

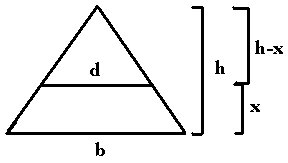
Obviously, the length of d is dependant on x. As x increases, d decreases. The main question is how to choose how high up, x, to cut so d is 'just right'. We will find out using a 'basic principles' approach.

In order to satisfy the constraints of the problem, we need

and

From the first constraint, we get

Solving for x, we get

From the second constraint, we get

Solving for x, we get

Setting these two values of x equal

and solving for d (ignoring nonsensical answers like negative lengths of pizza and pizza with no length), gives

Substituting this value of d back into either constraint, and solving for x, gives

Therefore, to make the cut fair, we cut up x = h(1-sqrt(2)/2) from the bottom

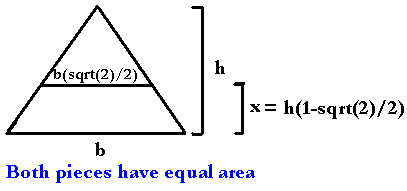
Next time you slice a piece of pizza, offer to slice it horizontally!

Additionally, if you and your friend are going to be enjoying an entire pizza (that is, a circle with radius r) you don't have to go through and slice each individual piece. Simply make a continuous circle cut going starting x = r(1-sqrt(2)/2) in from the outside. You get the outside ring shape with the crust, your friend gets the inner circle, and the ring and the circle have equal area.

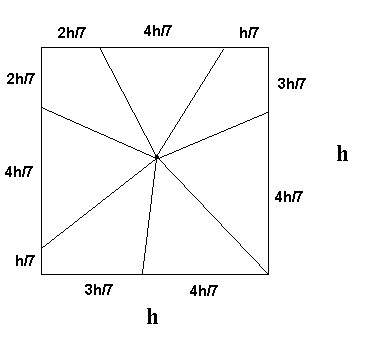
What about if the pizza is square? Let's say we have a square pizza of length h, and we want to divide it fairly between 7 people. The simplest answer is to cut vertical strips of pizza, such that the width of each strip is h²/7. However, what if we want to have triangular-ish pieces?

We know that

and since the height of any piece is just h/2

We want

Solving for base we get base = 4h/7. Therefore, to divide this square pizza fairly, simply cut the slices so the crust length (ie. base) for each slice is 4h/7.