Estimating the area of a unit circle

3/20/05

How do we know that pi = 3.14159... ? There are many ways to estimate pi to varying degrees of accuracy. My favorite ways use probability. This page demonstrates one such way: 'throwing darts'.

The only mathematics that you need to remember is how to calculate the distance a point is from the origin. A point in 2-dimensional space (an "x-y plane") is denoted by (x,y). The origin is (0,0). The distance (x,y) is from (0,0) is found by applying the Pythagorean Theorem to get (x-0)²+(y-0)² = r². Because we have a unit circle, r = 1, and we get distance from origin = sqrt(x² + y²). Then, just keep track of the number of times the point falls inside the circle, that is, when sqrt(x²+y²) < 1.

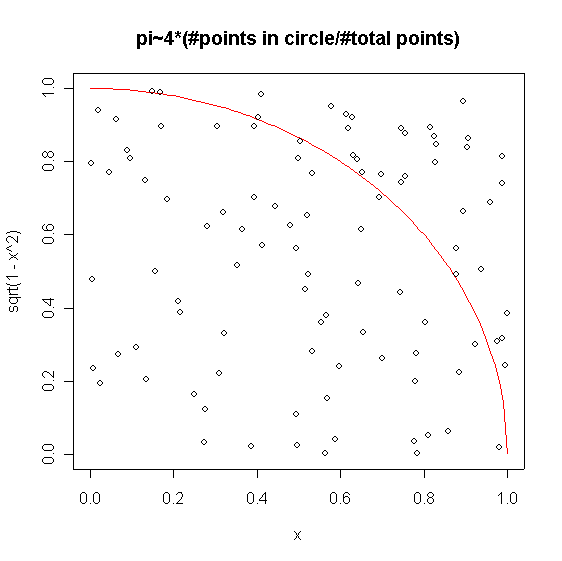
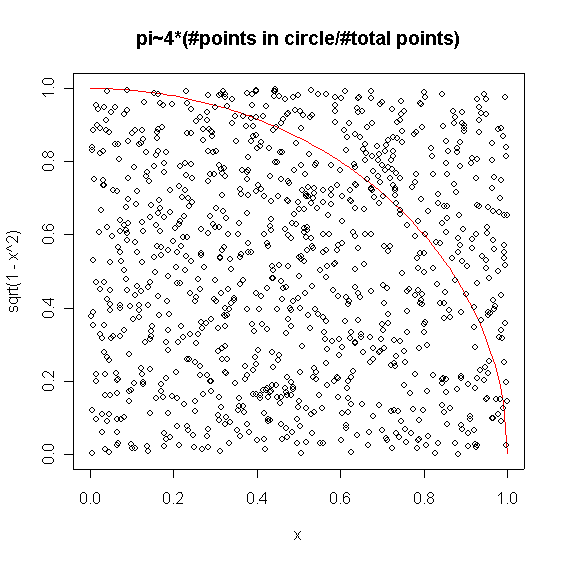
On this page I present an R script for calculating the area of a unit circle (ie. pi) by 'throwing' random points at a quarter of a circle. Using the ratio (#points in circle/#total points), we can estimate the area of the entire circle, pi, as pihat = 4*(#points in circle/#total points).

Here is my R script with comments

#to estimate the area of a unit circle using random numbers
#points are thrown randomly (uniformly) at the upper right quadrant of a unit circle
#pi is estimated as pihat = 4*(#points in circle/#total points)
n<-10000
a<-0
vec<-vector(mode="numeric", length=n)
x<-runif(n)
y<-runif(n)
#calculates the distance a point is from the origin
DistFromOrigin<-sqrt(x^2+y^2)
for (i in 1:n) {
if (DistFromOrigin[i]<1) (a<-a+1)
}
pihat<-4*(a/n)
#outputs the number of points and the estimate of pi
c(n,pihat)
#graphs the quarter circle
curve(sqrt(1-x^2),0,1,col="red")
#graphs the points
points(x,y)
title("pi~4*(#points in circle/#total points)")

And here are some graphs this script produced for various n.

The others scripts I ran for n=100,000 and n=1,000,000, produced pihat=3.13944 and pihat=3.142488 respectively. I've omitted those graphs, as they were essentially all black.