Decision Augmentation Theory: A Critique

10/2/05

Parapsychology is a very controversial area. Skeptics have called it a pseudo-science and proponents state that it is not. Regardless, I think all parties can agree it is fascinating, as there could be something real there or it could be a large-scale example of wishful thinking.

There are many areas in parapsychology one could focus on. For this informal article I chose to look at Decision Augmentation Theory (DAT).

What do proponents think is really going on when someone influences an outcome? There are two main schools of thought

• Force
• Information

The Force school holds that the brain literally reaches out somehow and nudges an object to alter its physical state. This is probably the popular conception of psychokinesis (PK). Just as experiments have moved from large objects to bitstreams, I expect more and more proponents to move from this school of thought.

The Information school holds that the brain somehow knows when to do something. It enters the bitstream at the right time to produce statistically significant results. This is DAT.

There is a third possibility of course: Chance. This is the idea that the results are due to chance. Again, for sake of brevity I'm assuming all experiments are sound, but this may not be the case in reality. This is ultimately the school many skeptics belong to because even if the experiments are sound, the results are not compelling.

A few years or so ago I looked at papers on DAT in some detail. They were an attempt to give some mathematical formalism to PK, and devise a way to see if Force, Information, or Chance is the best explanation for the results.. There are several papers on DAT that are worth reading. If you don't understand the mathematical details, that is OK. I think it is sufficient to understand the Force, Information, and Chance models, and get an idea of what you'd expect the scatterplot to look like for each one. Reading those papers will give you a better understanding of the following discussion.

The idea for seeing which of Force, Information, or Chance is responsible for the results is to graph the pairs of points (n, z^2) for each experiment, do some type of linear regression, see the magnitude of the slope and intercept, and see if the slope and/or intercept are statistically significant. The following table shows what you'd expect to see if Force, Information, or Chance were operating based on looking at the slope and intercept of the regression line

Note: in the table above "> 0" means statistically larger than 0, and "0" means statistically indistinguishable from 0, etc.

I have some Perl code which generates bitstreams of random length (out of 100000), to represent different hypothetical experiments (for 10, 100, 500, 1000, and 10000 experiments respectively), makes a scatterplot of (n, z^2) for each experiment, carries out a linear regression, and sees if the slope and intercept are statistically significant.

I didn't want to make things overly complicated, so I developed some very basic criteria to determine if the slope and intercept coefficient were statistically significant (and therefore the output is 'non-random'). My criteria were as follows

Here are some results for various number of experiments (called "trials" in the graph). The black line is what you'd expect by chance. The red line is the regression line

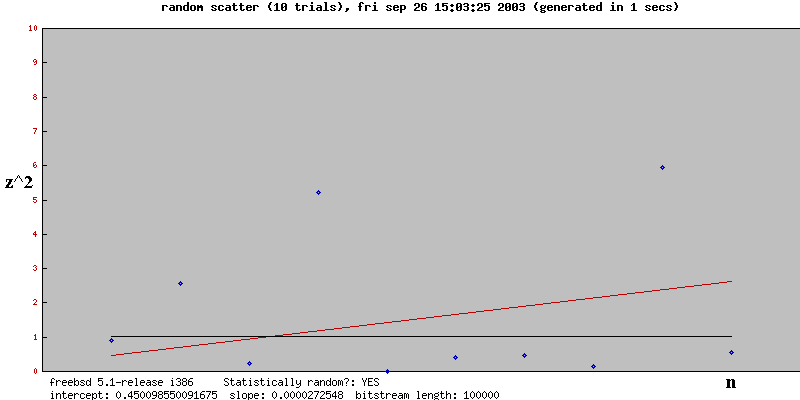
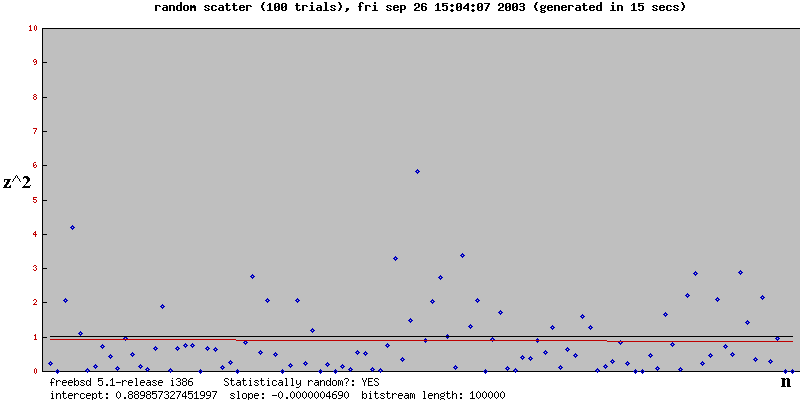
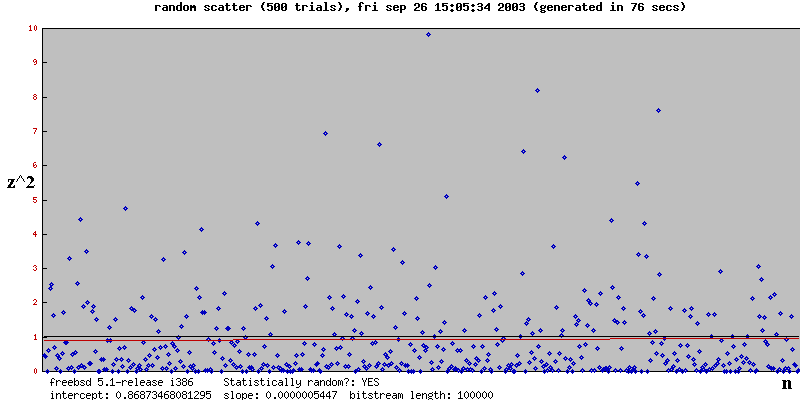
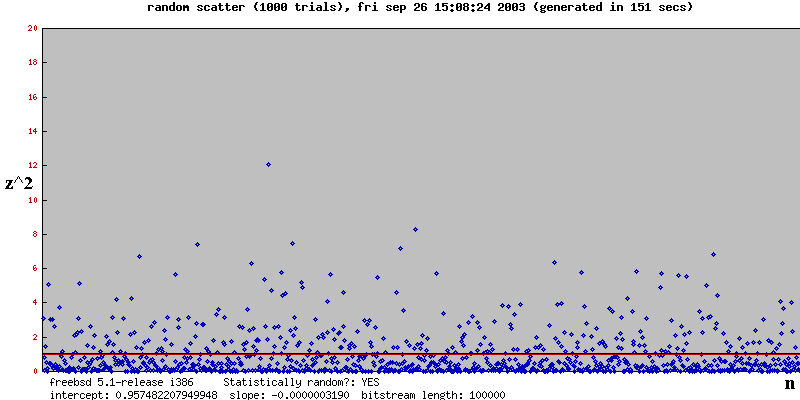
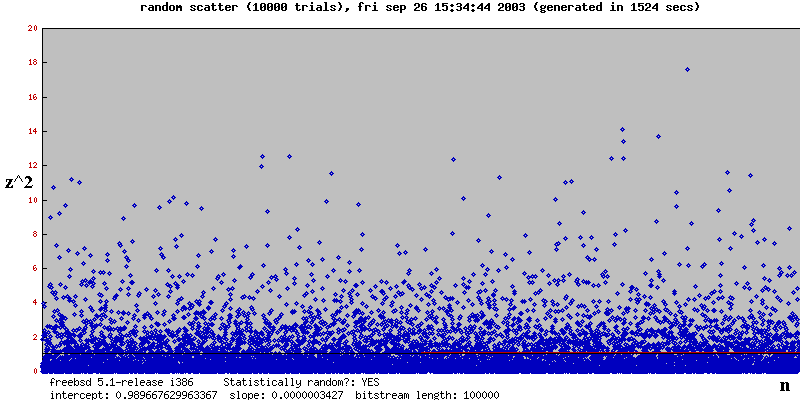
Note that for each scatterplot the result was best explained by Chance, and as the number of experiments increases, the regression line's slope tends towards 0 and the intercept tends toward 1. That is, the red line overlaps the black line, which is exactly what you'd expect if Chance were the explanation.

If PK is not real, then plotting the (n, z²), doing some type of linear regression, and seeing if the slope and/or intercept are statistically significant simply reduces the procedure to a not-so-powerful test for non-randomness.