If you find any of this useful, please consider donating via PayPal to help keep this site going.

Email news@statisticool.com to sign up to receive news and updates



The College Mathematics Journal, Vol. 31, No. 5, Nov. 2000, problem 688, p. 409

11/2000

Let an, n>=1 denote a sequence of positive real numbers, and for each n>=1, define rn to be the unique positive solution to the equation

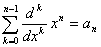
Given a nonnegative number L, characterize those sequences an such that lim n-->oo an = L.


Hint:

I created the following problem while I was playing around with some graphs. Consider graphing the following equations:

  1. y = x2 + 2x, y = 2
  2. y = x3 + 3x2 + 6x, y = 6
  3. y = x4 + 4x3 + 12x2 + 24x, y = 24
  4. y = x5 + 5x4 + 20x3 + 60x2 + 120x, y = 120
etc. (those familiar with differentation of polynomials will notice the pattern)

Notice that the x value of the intersection for each pair of equations decreases. However, if the process were continued, we know the x value of the intersection would not be 0, because we'd have

0 = really large number

which is not possible. Therefore the x value must be greater than 0, but what x value is it?

Here is the correspondence I have on the problem:

Please anonymously VOTE on the content you have just read:

Like:
Dislike:




If you enjoyed any of my content, please consider supporting it in a variety of ways:

AFFILIATE LINK DISCLOSURE: Some links included on this page may be affiliate links. If you purchase a product or service with the affiliate link provided I may receive a small commission (at no additional charge to you). Thank you for the support!