The Flawed Reasoning Behind The Flawed Reasoning Behind the Replication Crisis

8/5/19

In this article, I will explain several errors in reasoning in The Flawed Reasoning Behind the Replication Crisis, by Aubrey Clayton. The majority of content here is simply a copy-paste-edit from my Objections to Frequentism (which has a lot more information).

First, the simple Bayes Theorem, despite the name, is not inherently Bayesian as the article portrays. It is, in fact, fully in the frequentist statistics domain and is a basic result from the multiplication rule and conditional probability. The equation is P(A|B) = [P(B|A)P(A)]/P(B), where A and B are general events. Where Bayes Theorem becomes "Bayesian" is where the P(A) is a probability distribution for a parameter, and definitely "Bayesian" where the P(A) is based, not on prior experiment or objectivity, but on subjectivity. Moreover, if you are "tallying up historical murder records" (ie. frequencies) to get your prior, as an example in the article does, are you doing Bayesian statistics or frequentist statistics?

One issue I see in the article, is that it uses a common, but incorrect, definition of "replication crisis", which is that the effect size, or statistic, or general results of a current study did not match or reproduce those of a previous similarly designed study. However, that is not the standard experimental design definition of a "replication". The only thing "replication" means in experimental design is that the similarly designed study was conducted, and not that it obtained a similar effect size or statistic as a previous similarly designed study. In other words, if the replication "goes the other way", that is actually good information for scientific knowledge, and not a "crisis" which is the standard narrative.

Regarding the claim that the "replication crisis" was/is caused by frequentist null hypothesis significance testing, everyone knows that a replication is technically never absolutely identical to another replication. In real life, we come as close as we can in the experimental setup. Plus, we are working with data that has a stochastic element to it. No matter if frequentist or Bayesian, no matter how well designed the experiments, our decisions will have errors associated with them because of this fact of nature.

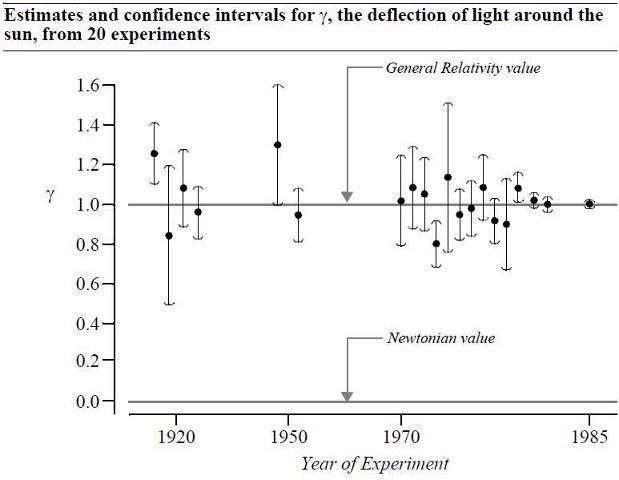
The article, and much other criticism of frequentism, mainly discusses single experiments, as if single experiments, using any method, mean much of anything. Consider my "go to" graph below, and ask yourself if a single experiment would have changed your mind. Now, consider the data as a whole, over time and/or a meta-analysis; quite a different picture emerges

One could argue as Mayo does that the "attitude fostered by the Bayesian likelihood principle is largely responsible for irreplication". That is, it can be argued that it tends to foster the ideas that we don't have to worry about selection effects and multiple testing if we use Bayesian methods. She also writes "Misinterpretations and abuses of tests, warned against by the very founders of the tools, shouldn't be the basis for supplanting them with methods unable or less able to assess, control, and alert us to erroneous interpretations of data" as well as "Don't throw out the error control baby with the bad statistics bathwater". I strongly recommend her Statistical Inference as Severe Testing: How to Get Beyond the Statistics Wars.

The reliance on the diagnostic screening interpretation of probability has issues, mainly because of "crud factors" in different fields (for example, is it a "replication crisis" or actually just a "psychology crisis"?) It is true that paying attention to "base rates" is important, so I would have thought that the author would have done the same by paying attention to the numerous examples of frequentist statistics doing good in the world, rather than focusing only on a few counterexamples. The false positive rate work by Cohen, Colquhoun, and others, are attempts to derive the probability that a statistically significant result was a false positive, and that the false positive is large even for reasonable assumptions. Unfortunately, the assumptions aren't that reasonable. They tend to be based on interpreting the p-value found in a single test, which is only an indication, as well as can be sensitive to the prior. These Bayesian/screening/likelihood interpretations of frequentist significance testing are admittingly somewhat seductive because they seem true and are based on simple arithmetic. Hagen discussed this a little in In Praise of the Null Hypothesis Statistical Test. In one of Hagen's examples, from Cohen, he merely considers one replication using P(H0|sig test) from the previous experiment. After a few replications, the so-called false positive rate argument is completely moot. Are we to believe that a critique of frequentist significance testing based on a single experiment should be taken seriously?

The article references John Ioannidis to support a Bayesian view. However, Ioannidis in his recent Retiring statistical significance would give bias a free pass article wrote

"Statistical significance sets a convenient obstacle to unfounded claims. In my view, removing the obstacle could promote bias. Irrefutable nonsense would rule."

The author writes "...a researcher can sift through many possible associations to find one that meets the threshold of significance...". This is true, but this is not a fault of frequentism, but of questionable research practices. A Bayesian could engage in the exact same questionable research practices with Bayes factors, prior-hacking, and so on. Any method can be hacked or gamed. Related to this is, I feel that critics believe they are critiquing frequentism, when in fact they are (rightly) critiquing arbitrary journal standards.

The author writes "In 2015, the journal Basic and Applied Social Psychology took the drastic measure of banning the use of significance testing in all its submissions..." But what were the effects after BASP banned the use of inferential statistics in 2015? Did science improve? Ricker et al in Assessing the Statistical Analyses Used in Basic and Applied Social Psychology After Their p-Value Ban write

In this article, we assess the 31 articles published in Basic and Applied Social Psychology (BASP) in 2016, which is one full year after the BASP editors banned the use of inferential statistics.... We found multiple instances of authors overstating conclusions beyond what the data would support if statistical significance had been considered. Readers would be largely unable to recognize this because the necessary information to do so was not readily available.

Also, please read So you banned p-values, how's that working out for you? by Lakens.

The author writes "...an editorial in Nature co-signed by more than 800 authors argued for abolishing the use of statistical significance altogether" I have no way of knowing if that 800 is, dare I say, significant or not. Should frequentists gather many more than 800 signatures? What would that show? Critics seem to be baffled why articles in Nature and ASA publications (and many other places) using "p<" and statistical significance terminology are already appearing after the publication of the Nature and ASA hit pieces.

The author writes "Furthermore, it may not matter too much exactly what prior probability we use." This is a selling point for frequentist statistics, because the likelihood can swamp the prior, for any prior. So to answer the author's question of "Imagine you or a loved one received a positive test result. Which summary would you find more relevant?" I would prefer the decision based on results from many well-designed experiments that eliminate subjectivity as much as possible.

Regarding "By ignoring the necessity of priors, significance testing opens the door to false positive results.", then by using priors, Bayesian statistics opens the door to more subjectivity, sensitivity analysis, potential bias, and hacking.

The article tries to equate subjective priors (probability distributions on parameters) with the general notion of subjectivity in subject matter expertise, judgments, and choice of likelihood. If the argument is that "everything is subjective", then the claim "everything is subjective" is itself subjective and therefore somewhat questionable.

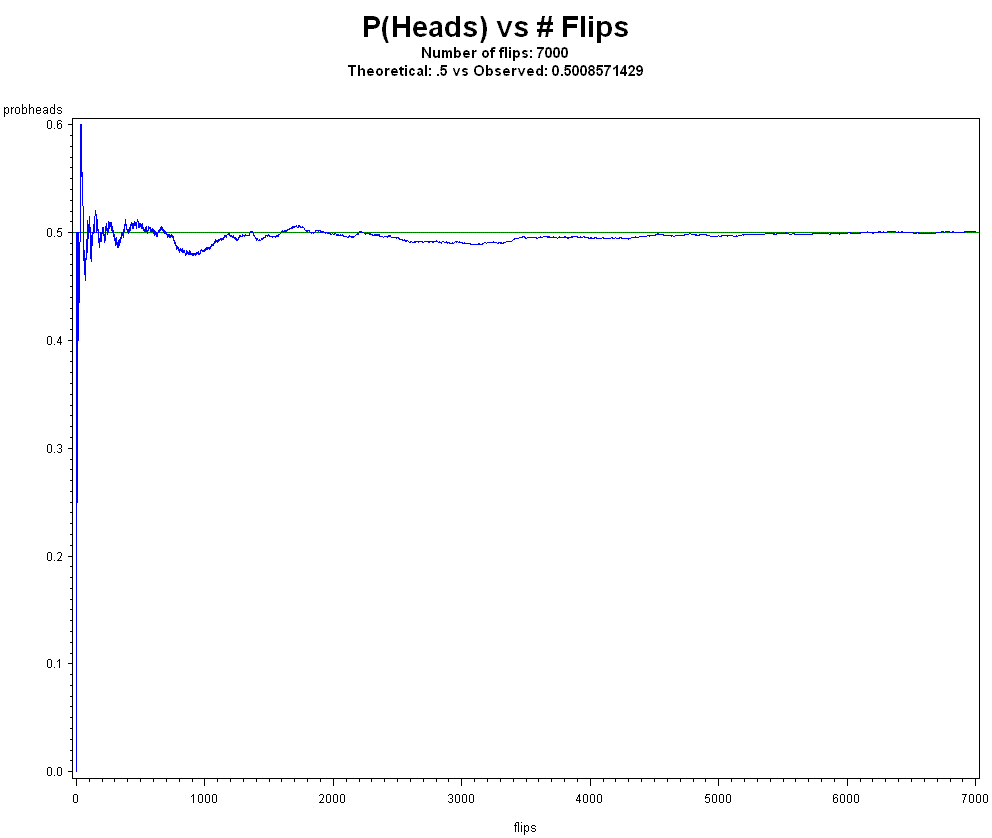
To illustrate the difference between subjective and objective, consider the Strong Law of Large Numbers (SLLN) which says that it is almost certain that between the m^th and n^th observations in a group of length n, the relative frequency of Heads will remain near the fixed value p, whatever p may be (ie. doesn't have to be 1/2), and be within the interval [p-e, p+e], for any small e > 0, provided that m and n are sufficiently large numbers. Anyone can flip a coin and observe the relative frequency of Heads tending to converge to a horizontal line as the number of flips increase.

Or, consider balls cascading down a quincunx or "Galton Board" to form an approximate normal distribution

Anyone, regardless of beliefs or Bayesian priors, can flip coins or tip over a Galton board and see the results.

Below I list a very small sample of some resources that are friendly to frequentism and/or significance testing for your reading pleasure:

• Probability, Statistics, and Truth, by von Mises
• Why I am Not a Likelihoodist, by Gandenberger
• Equivalence Testing for Psychological Research: A Tutorial, by Lakens et al
• What can psychology's statistics reformers learn from the error-statistical perspective?, by Haig
• Frequentism as Positivism: a three-sided interpretation of probability, by Lingamneni
• Bayesian Just-So Stories in Psychology and Neuroscience, by Bowers and Davis
• Is it Always Rational to Satisfy Savage's Axioms?, by Gilboa, Postlewaite, and Schmeidler
• Stopping rules matter to Bayesians too, by Steele
• Why optional stopping is a problem for Bayesians, by Heide and Grunwald
• HEP physics looking at p-values
• In defense of P values, by Murtaugh
• On the Birnbaum Argument for the Strong Likelihood Principle, by Mayo
• On Using Bayesian Methods to Address Small Sample Problems, by McNeish
• Will the ASA's Efforts to Improve Statistical Practice be Successful? Some Evidence to the Contrary, by Hubbard
• In Praise of the Null Hypothesis Statistical Test, by Hagen
• The practical alternative to the p-value is the correctly used p-value, by Lakens
• Use of significance test logic by scientists in a novel reasoning task, by Morey and Hoekstra
• On the Brittleness of Bayesian Inference, by Owhadi, Scovel, and Sullivan
• Qualitative Robustness in Bayesian Inference, by Owhadi and Scovel
• Bayesianism and Causality, or, Why I am Only a Half-Bayesian, by Pearl
• Why Isn't Everyone a Bayesian, by Efron
• Bayes Theorem in the Twenty-first Century, by Efron
• You May Believe You Are a Bayesian But You Are Probably Wrong, by Senn
• Statistical Inference as Severe Testing: How to Get Beyond the Statistics Wars ,by Mayo
• The Interplay of Bayesian and Frequentist Analysis, by Bayarri and Berger
• The case for frequentism in clinical trials, by Whitehead
• There is still a place for significance testing in clinical trials, by Cook et al

In my opinion, these "beware of dichotomania" or "retire statistical significance" type of articles need to be retired. They tend to promote fallacies, however subtle, ignore the good of frequentism and hypothesis testing in science and other areas, oversell Bayesian statistics by not mentioning any criticisms, and ignore the criticisms of proposed alternatives to hypothesis testing. The explicit or implicit claims that by using Bayesian statistics we will eliminate questionable research practices and improve replication do not hold up to scrutiny.

Oh, and the article also only mentions Fisher and not Neyman and Pearson.

Thanks for reading.