Plenary Session 2.06: Frequentist Response

8/7/19

In episode 2.06 of Plenary Session, Vinay Prasad interviewed Frank Harrell on Bayesian statistics. The interview starts at 27 minutes into the podcast.

First off, Harrell is a statistics O.G., and I agree with easily over 90% of what he says in general. We are "on the same team", trying to understand the world using experiments, data, logic, science, probability, and statistics, rather than using a crystal ball, tarot cards, or astrology. But, with that said, I believe he gives somewhat inaccurate information on frequentism in this podcast. This article will discuss some of what he said on the Plenary Session podcast.

Harrell said that probability means what you want it to mean. I definitely disagree with this. Much like a specific science limits their field of study to be well-defined, frequentism purposefully limits probability to be long-term relative frequency instead of admitting any type of general uncertainty to be the same status as probability. Like von Mises, I am fine with "chance", "belief", or "uncertainty" being used to mean other types of probability-like things. This is not to say that studying non-relative frequency interpretations is unimportant, or that you shouldn't learn about it or do it, however. Harrell justifies his probability means what you want it to mean statement by referring to Kolmogorov's axioms. However, when going from the mathematical to the real world, Kolmogorov himself noted in his On Tables of Random Numbers the contribution of von Mises

"...the basis for the applicability of the results of the mathematical theory of probability to real 'random phenomena' must depend on some form of the frequency concept of probability, the unavoidable nature of which has been established by von Mises in a spirited manner."

As well as in his Foundations of the Theory of Probability

"In establishing the premises necessary for the applicability of the theory of probability to the world of actual events, the author has used, in large measure, the work of R. v. Mises"

Regarding one time events like what is P(world war III) as showing a flaw in frequentism (I note that Harrell did not provide a Bayesian answer either), these type of questions are not a deal breaker. First, no approaches of probability or statistics have very satisfactory answers for n = 1 or small sample or one-time events in my opinion. In some cases a frequentist can assign probability to single events using a prediction rule. For example, P(A_n+1) = xbar_n, where it is just a matter of choosing an appropriate statistical model, as Spanos notes, and making your assumptions known. For example, one could model the economies of the world, the relation between countries, measures of aggression, weapon supplies, war-like activities, and so on. There is also a "many worlds" interpretation of frequentism that I will mention just to be complete, and that refers to the "sci-fi" idea that say for a one-time event with probability p = X/N, the event occurred in X worlds out of the N worlds, and this one-time event just happened to occur in our world. The frequentist could also simply use Bayes rule, which is fully in the frequentist domain when it involves general events and not probability distributions on parameters.

Regarding Harrell claiming that Bayesians can stop whenever, just because one can doesn't mean one should. In Stopping rules matter to Bayesians too, Steele writes

"If a drug company presents some results to us - "a sample of n patients showed that drug X was more effective than drug Y" - and this sample could i) have had size n fixed in advance, or ii) been generated via an optional stopping test that was 'stacked' in favour of accepting drug X as more effective - do we care which of these was the case? Do we think it is relevant to ask the drug company what sort of test they performed when making our final assessment of the hypotheses? If the answer to this question is 'yes', then the Bayesian approach seems to be wrong-headed or at least deficient in some way."

Also, see Why optional stopping is a problem for Bayesians, by Heide and Grunwald.

Harrell mentions that biostatisticians use Bayesian statistics to determine if a drug is efficacious, however, determining efficacy of drugs is what frequentist statistics does all the time in biostatistics as well, especially in Phase III trials. In The case for frequentism in clinical trials, Whitehead writes

"What of pure Bayesian methods, in which all conclusions are drawn from the posterior distribution, and no loss functions are specified? I believe that such methods have no role to play in the conduct or interpretation of clinical trials."
...
"The argument that in a large trial, the prior will be lost amongst the real data, makes we wonder why one should wish to use it at all."
...
"It disturbs me most that the Bayesian analysis is unaffected by the stopping rule."
...
"I do not believe that the pure Bayesian is allowed to intervene in a clinical trial, and then to treat the posterior distribution so obtained without reference to the stopping rule."

Also, in There is still a place for significance testing in clinical trials, by Cook et al, they say (bolding mine)

"The carefully designed clinical trial based on a traditional statistical testing framework has served as the benchmark for many decades. It enjoys broad support in both the academic and policy communities. There is no competing paradigm that has to date achieved such broad support. The proposals for abandoning p-values altogether often suggest adopting the exclusive use of Bayesian methods. For these proposals to be convincing, it is essential their presumed superior attributes be demonstrated without sacrificing the clear merits of the traditional framework. Many of us have dabbled with Bayesian approaches and find them to be useful for certain aspects of clinical trial design and analysis, but still tend to default to the conventional approach notwithstanding its limitations. While attractive in principle, the reality of regularly using Bayesian approaches on important clinical trials has been substantially less appealing - hence their lack of widespread uptake."
...
"It is naive to suggest that banning statistical testing and replacing it with greater use of confidence intervals, or Bayesian methods, or whatever, will resolve any of these widespread interpretive problems. Even the more modest proposal of dropping the concept of 'statistical significance' when conducting statistical tests could make things worse. By removing the prespecified significance level, typically 5%, interpretation could become completely arbitrary. It will also not stop data-dredging, selective reporting, or the numerous other ways in which data analytic strategies can result in grossly misleading conclusions."

Also see Adaptive Designs for Clinical trials, by Bhatt and Mehta. Harrell is quite right that multiple endpoints and adjustments make for more difficult math for the frequentist, absolutely (which is odd then when he contradicts that by arguing elsewhere that frequentism has easier mathematics). Harrell said whereas frequentists, you're saying if the drug has no effect, what is the probability of the data being this surprising or more surprising. I would opine that when a frequentist gets a p-value, they are not focusing on it so much as a probability per se like Harrell suggests. A p-value is simply a scaling of the distance the observed test statistic is from what you'd expect under a model. Moreover, a p-value is just one of many things frequentists can look at. What Harrell actually seems to be arguing against is modus tollens (MT) logic, or argument by counterfactual/contradiction/falsification logic. The logic of modus tollens says P->Q, and if we observe not Q, therefore we conclude not P. Note that P is the null hypothesis H0, and Q is what we'd expect the test statistic T to be under H0. A concrete example is, we agree on assuming a fair coin model. We therefore expect about 50 heads if we flip a coin 100 times. However, we observe 96 heads (96 put on a p-value scale would be an extremely small p-value). Say we also repeat this experiment 3 times and observe 92, 95, and 89 heads. Therefore, we conclude the fair coin model is not good. This type of logical argument is valid and essential for falsification and good science a la Popper. Anticipating the question, yes, MT reasoning is still valid when put in probability terms. Modus tollens, and modus ponens, put in terms of probability effectively introduce bounds, much like in linear programming. See Boole's Logic and Probability by Hailperin, and Modus Tollens Probabilized by Wagner.

This MT reasoning, Harrell says is a transposed conditional, and therefore a fallacy. However, regarding a claim like everyone really wants P(H0|data), even conceding this point to be true just for sake of argument, one realizes after some thought that one only gets this if they allow subjective probabilities to enter, so they can't really ever get this. That is, Bayesians cannot get at P(H0|data) either but only at P(H0|data, my subjective beliefs), or Belief(H0|data), which is not quite the same thing. Therefore, one has to instead focus on P(data|H0) and use modus tollens logic. People confusing one probability with the other is actually the error of the transposed conditional. However, frequentists are not confusing one with the other and frequentists are not after P(H0|data) anyway. The host then said that "what we actually care about is does this drug offer a benefit", to which Harrell said "exactly right", which is great, because that is what a confidence interval would tell you or some type of estimation. And again, frequentists are not confined to only using p-values.

Regarding the host saying "we are all Bayesians" and "no one is truly a frequentist", and Harrell partially agreeing, this is not correct. Just because one has a belief about something, or uses subjectivity in some way, or background knowledge, doesn't mean one would want to therefore put a mathematical object (ie prior) on a parameter.

Harrell said there is no mathematical theory on how multiplicity adjustments are done and multiplicity adjustments are completely ad hoc. Tukey, Scheffe, and others, in fact, worked out the basic mathematics long ago, and others are continuing it in the present day for more difficult situations, so I'm not sure why Harrell says there is no mathematical theory. The theory is simply that as we do more comparisons, we are more likely to reject null hypotheses erroneously, so we need to try to lessen those errors. Actually, we need to do that while taking type II errors, power, sample size, cost, and a variety of other factors, into account. There are indeed a lot of different types of adjustment methods with their own pros and cons and situations that could call for adjustments, so I would say a solution to prevent the "ad hoc" feel is to have the adjustments pre-specified whenever possible. As far as "ad hoc", the word itself just means as needed, so yes, we should adjust as needed to be doing more sound statistics instead of ignoring them. Doing a quick search for "multiplicity adjustments" and "biostatistics" shows me that they are the norm in biostatistics (and experimental design in general). There are many newer resources, but a few decent ones to get the general flavor are the FDA's Multiple Endpoints in Clinical Trials Guidance for Industry, and Introduction to Multiplicity in Clinical Trials, by Novartis. Harrell mentions something like comparing A to B should have no influence on comparing C to D. This gets at pairwise tests based on joint rankings vs pairwise tests based on separate rankings (and Harrell, if he had to suffer doing these adjustments, apparently favors separate rankings, which is OK). However, Lehmann mentions that a joint ranking uses of all the information in an experiment, namely the spacings between all points, which is lost in a separate ranking procedure. For some data, the separate ranking procedures can perform poorly.

Harrell says with Bayes you have a way to say how relevant do you want to allow the previous data [to be -J]. However, with frequentism, you can do this as well. For example, you could simply append various datasets together. Or, most likely, you would do a meta analysis, and each contributing result could be weighted by 1/variance or some other way.

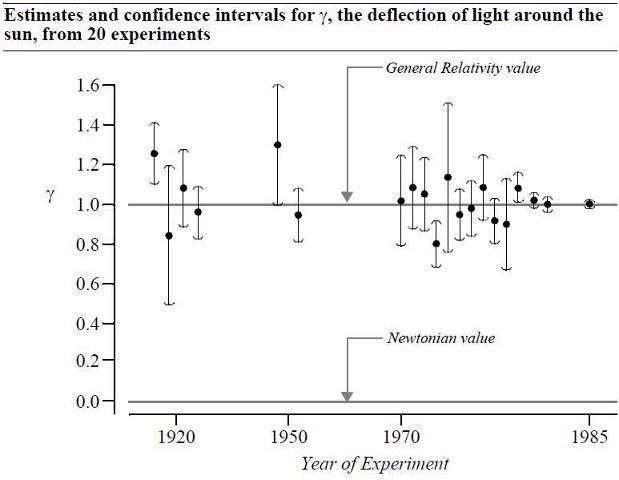
For one study they discussed, different priors changed the posterior drastically, the posterior probability ranging from .05 to .70 to .998 (let's just say from 0 to 1). This is like a "Drake equation", where even if the mathematics is correct (it is), the user can get just about any output, and hence decision, based on their inputs. When inputs are very subjective, this is an issue. For example, in one paper on ESP experiments, Jahn, Dunne, and Nelson write

"Whereas a classical analysis returns results that depend only on the experimental design, Bayesian results range from confirmation of the classical analysis to complete refutation, depending on the choice of prior."

Harrell says Bayesian evidence assessments are directional and compares this to the flaws of a frequentist 2-sided p-value. This is odd, since frequentists can and regularly do 1-sided (ie. directional) tests. Also check out OneSided.org, by Georgiev.

Harrell says you're bringing in other factors, you're not just playing the odds to discuss the fact that people bring in subjectivity, personal beliefs, opinions, outside information, etc., into a decision (although later he says we just play the odds crossing the street, etc.). That all is true, but it doesn't mean that doing so is always beneficial (like taking stock tips from a shoeshine boy), and doesn't equate to a need for doing a Bayesian analysis. To compare using Bayesian priors, which are putting possibly subjective probability distributions on parameters to using any inputs for an analysis and saying something like "well, both are the same thing really" is simply mistaken. If something like "everything is subjective" is true, then the claim "everything is subjective" is itself subjective and therefore I doubt it very much. Arguably the main purpose of science is to be objective as possible. Bringing in the right things (again, which can be done without priors) is what is important, like subject matter expertise and scientific knowledge, to get the most accurate odds to make decisions.

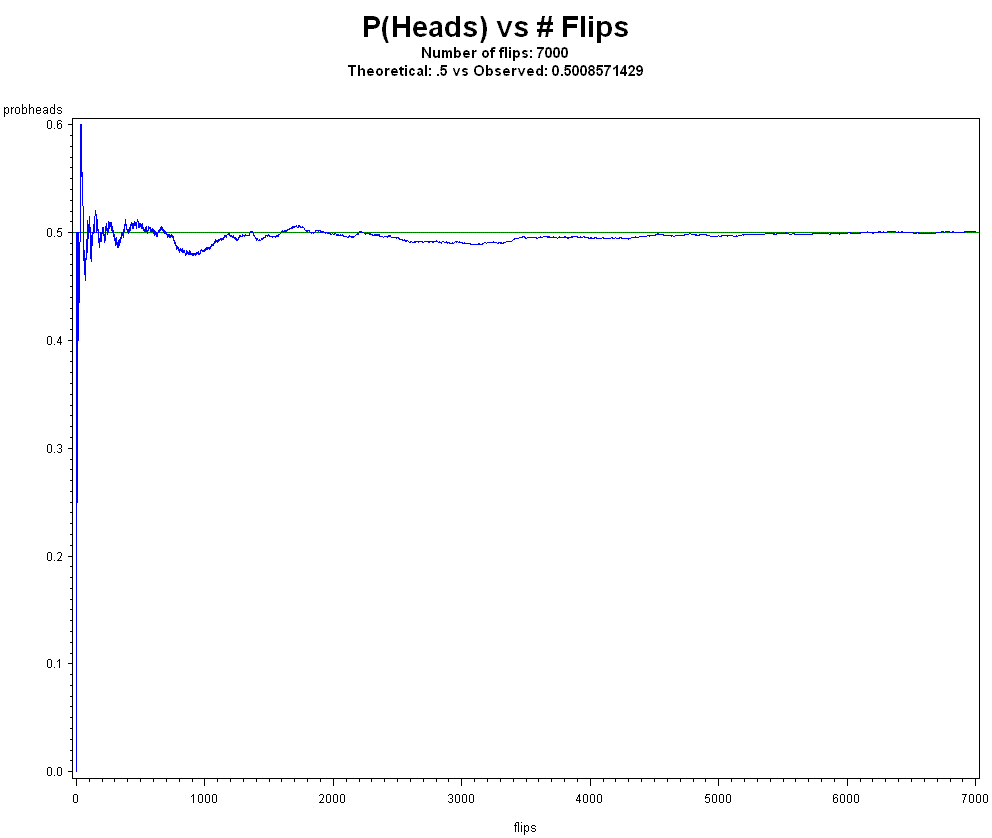
Harrell says the absence of evidence is not evidence of absence which is a good skeptical maxim in general, but I feel he misapplies it here. He continues the p-value brings evidence against something and never in favor of anything. But consider what your decision would be if you assume a fair coin model, do 100 flips say for 5 trials, and get 47, 48, 51, 50, and 54 heads. This is strong evidence (not proof, in science we don't talk about proof) that the coin is indeed a fair coin. This reasoning is used often successfully in quality control, for example. This works, in general, because the parameter space is exhausted and the experiments are sound and replicated. And, again, frequentism is more than just p-values.

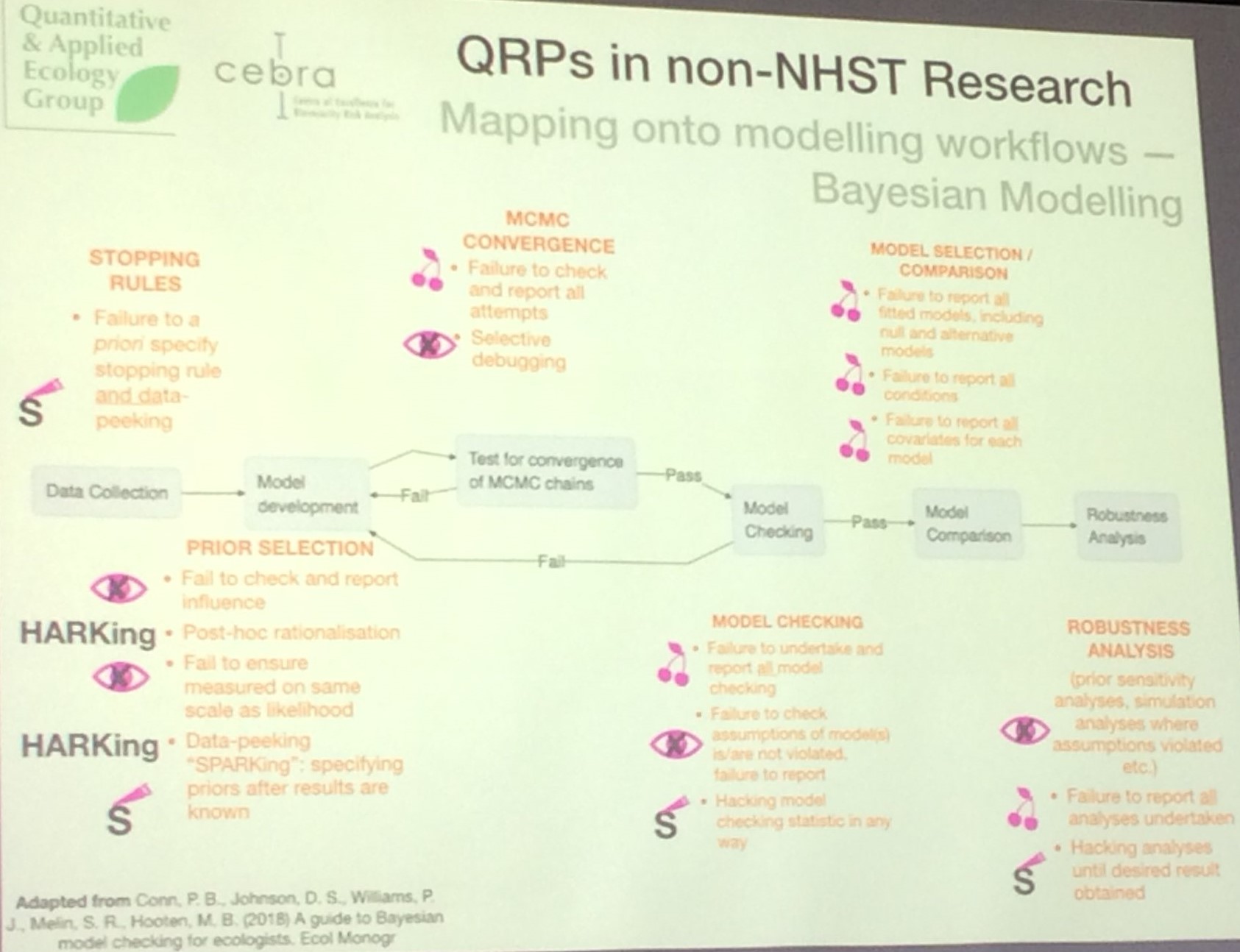
I don't agree that using Bayesian methods would necessarily lower the amount of gaming. Bayesians would have similar things to game, data editing, as well as prior hacking, MCMC settings, sensitivity analysis choices, BF cutoffs, and the ignoring of multiplicity adjustments and stopping rules. Ultimately the people engaging in QRPs are at fault, not the methods. On non-NHST research, Elise Gould said "Non-NHST research is just as susceptible to QRPs as NHST."

Harrell says with Bayes you can decide at any point you have enough evidence and can trigger a successful trial or determination of utility. Frequentists can too with sequential analysis, adaptive design, or meta analysis.

Harrell says Bayesians are calculating the probability of efficacy, but frequentists can get at efficacy by estimation of effects and confidence intervals from well-designed replicated experiments and meta analysis.

Regarding dichotomization, dichotomania, etc., the claim that making decisions from a p-value being less than an alpha is "rigid" and therefore bad are overblown. It is actually rigid and therefore good. First, frequentism is not only null hypothesis significance testing. Second, alpha is not "arbitrary" as Harrell claims, but should be based on cost of making a type I error for your study, sample size, necessary adjustments and so on, and there are many methods to do this. Interestingly enough, the typical alpha=.05 is not even as arbitrary as is often charged. Fisher basically said it was convenient, and resulted in a z-score of about 2, and made tables in his books (pre-computer times) easier. But, Fisher knew and wrote about that it roughly corresponded to previous scientific conventions of using probable error (PE) instead of standard deviation (SD). The PE is the deviation from both sides of the central tendency (say a mean) such that 50% of the observations are in that range. Galton wrote about Q, the semi-interquartile range, defined as (Q3-Q1)/2, which is PE, where Q3 is the 75th percentile and Q1 is the 25th percentile. For a normal distribution, PE ~ (2/3)*SD. Written another way, 3PE ~ 2SD (or a z-score of 2). The notion of observations being 3PE away from the mean as very improbable and hence "statistically significant" was essentially used by De Moivre, Quetelet, Galton, Karl Pearson, Gosset, Fisher, and others, and represents experience from statisticians and scientists, not just a plucking out of thin air. See On the Origins of the .05 Level of Statistical Significance, by Cowles and Davis.

On the idea of getting rid of frequentist methods, Mayo writes

"Misinterpretations and abuses of tests, warned against by the very founders of the tools, shouldn't be the basis for supplanting them with methods unable or less able to assess, control, and alert us to erroneous interpretations of data"

and

"Don't throw out the error control baby with the bad statistics bathwater"

Ioannidis in his recent Retiring statistical significance would give bias a free pass wrote

"Statistical significance sets a convenient obstacle to unfounded claims. In my view, removing the obstacle could promote bias. Irrefutable nonsense would rule."

As a concrete example, what were the effects after BASP banned the use of inferential statistics in 2015? Did science improve? Ricker et al in Assessing the Statistical Analyses Used in Basic and Applied Social Psychology After Their p-Value Ban write

"In this article, we assess the 31 articles published in Basic and Applied Social Psychology (BASP) in 2016, which is one full year after the BASP editors banned the use of inferential statistics.... We found multiple instances of authors overstating conclusions beyond what the data would support if statistical significance had been considered. Readers would be largely unable to recognize this because the necessary information to do so was not readily available."

Also, please read So you banned p-values, how's that working out for you? by Lakens.

Harrell says anything we do with samples spaces...is going to be problematic which is hilarious. Sound decisions are made all the time in survey sampling, for example. The sampling distribution is an important ingredient for objectivity. Not to mention, this contradicts his previous justification of appealing to Kolmogorov's axioms, since those axioms first assume a sample space.

Harrell says we have serious publication bias in the literature. I agree, but this isn't a fault of any statistical method but arbitrary journal requirements and publish or perish and QRPs. One can play games with p-values, with Bayes factors, or with any other arbitrary journal requirement.

Harrell says inference and making yes/no decisions is not how humans live for the most part. We actually live by playing the odds. I would say both really, as well as other non-probability methods. For his example "do you cross a busy street?", this can be answered by playing the odds, but also by frequencies, knowledge of physics, biology, costs/utility/economics, and other methods. Answering it with frequencies, I know, for example, that everyone I read about who got hit by a car has died or been severely injured, so if I decide to cross I will cross at the crosswalk, be cautious, look both ways, etc. The examples Harrell gives of "playing the odds" can be put in frequentist terms pretty easily without needing a posterior distribution. Moreover, learning about the world via science and inference differs from "how we live" in a lot of ways. Understanding to be cautious to cross the street is not as rigorous a process as determining the efficacy of medicines.

Bayes methods can address measurement error, as Harrell notes. However, this can also be done by frequentist methods. This can be done using regression or imputation, for example. Also, Deming, Kish, Groves, Biemer, Gy, and many others have looked at measurement error (and dozens of other errors beyond sampling error) in what is called a total survey error approach.

I strongly recommend Mayo's Statistical Inference as Severe Testing: How to Get Beyond the Statistics Wars. It is by far the best book out there on understanding frequentism, Bayesian, science, inference, philosophy, and related issues.

Thanks for reading.