A Closer Look at Han Solo Bayes

6/23/18

In Count Bayesie's excellent article "Han Solo and Bayesian Priors", he has a nice example showing the basics of Bayesian reasoning and the advantages of using a prior. However, while showing the basics of Bayesian reasoning, it also shows the basic flaws in Bayesian reasoning, namely the flaws of using priors. In this article I will explain why this is so.

Please check out his book Bayesian Statistics the Fun Way: Understanding Statistics and Probability with Star Wars, LEGO, and Rubber Ducks

The background is we are watching The Empire Strikes Back!:

• They are about to fly into an asteroid field
• C3PO says "Sir, the possibility of successfully navigating an asteroid field is approximately 3,720 to 1!" (Count Bayesie makes this 7440 and 2)
• Han Solo says "Never tell me the odds!" and goes in...
• ...Han Solo makes it!

OK. So Count Bayesie takes what C3PO says as the likelihood and that P(RateOfSuccess|Successes) = Beta(alpha, beta) = Beta(2, 7440). We will assume that this is correct for now.

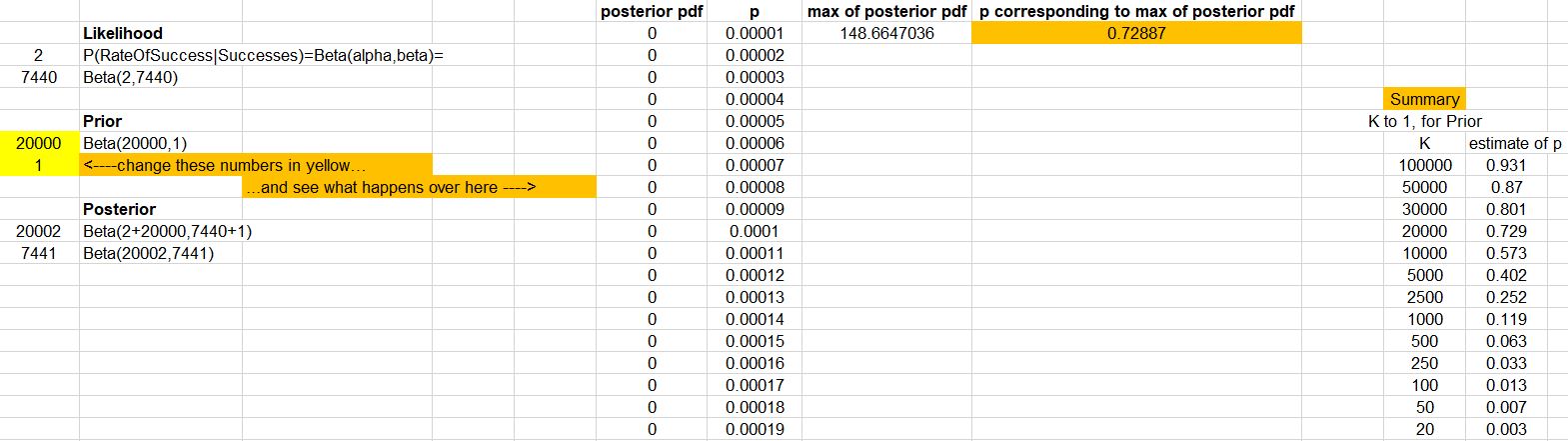
Next, Count Bayesie talks about priors and tries to convince you that you need them, but I am not convinced. He mentions "believe" or "belief" about 10 times in the paragraphs in this section. In fact, his choice of prior seems to be backed up by "I personally feel..." and "I'm going to say I roughly feel that...". Count Bayesie assigns a prior with a ton of weight on Han Solo being successful, a Beta(20000,1). One question is, if you're assigning that much weight on success, why even bother to calculate a posterior in the first place? Also, what if others feel differently? What if their feelings totally contradict yours? What if different priors completely change the posterior? Spoiler: they can and often do. Can everyone be right?

The choice of likelihood and prior were also done to make calculations for the posterior easier, ie. the so-called conjugate priors. I personally don't get spending time to justify a likelihood and a prior and then basically say that was all really for our convenience of calculation. Those two things don't really jive. In any case, the posterior comes out to be Beta(alpha_posterior, beta_posterior) = Beta(alpha_likelihood+alpha_prior, beta_likelihood+beta_prior). In our specific case, this is a Beta(2+20000, 7440+1), and most of the weight of this posterior distribution is around p=.73, to conclude that Han Solo has ~73% chance of making it.

As mentioned, my beliefs could differ from yours. Let's do a quick exercise. Raise your hand if you know people whose beliefs differ from yours. Everyone's hand up? I thought so. So what if, instead, I feel a prior of Beta(10000,1)? Then most of the weight of the posterior is around p=.57. A prior of Beta(500,1)? Then p=.063. The posterior could literally be all over the place.

Some Bayesians talk about "p-hacking" that is supposedly rampant in statistics, with the implication being that it is rampant in Frequentist statistics. P-hacking is basically the practice of analyzing data in ways to yield a desired target result, specifically a statistically significant p-value. However, the same exact thing could be done in Bayesian statistics, but even more so, because now we have unlimited priors to hack with. It could still be called "p-hacking", but this time the p would also stand for "prior". We could simply choose a prior to help yield the posterior result we'd like to see. The root cause of p-hacking, of course, is not about Frequentism or Bayesian, but a matter of ethics, but I just thought I'd point that out.

A big issue in this case, like Count Bayesie pointed out, is that C3PO's data is on all pilots without any other context, so I doubt it is the correct likelihood in the first place. If C3PO had data on pilots with similar training, skills, and ships of Han Solo, or data on the different types of asteroid fields (surely they are not all the same), then his probability would be different. Sure, one can make any assumptions with priors (the parameters and hyperparameters and the choice to make them conjugate), plug and chug, and get numbers, but I'm not sure if they have any meaning whatsoever as a "probability". Maybe "personal chance" would be a better term for it. It would most likely be best to get more data and use the likelihood, since we know as more data is obtained the likelihood swamps the prior.

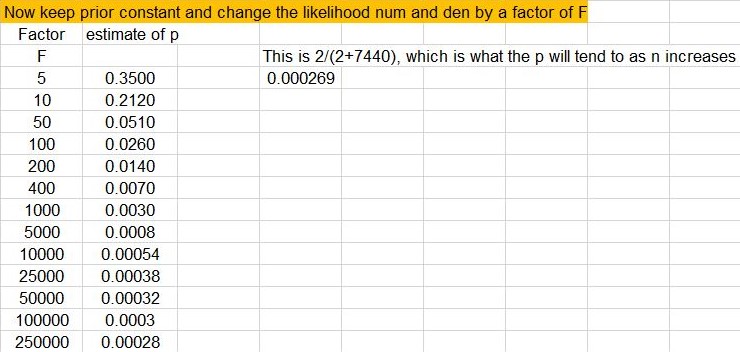
For example, keeping the prior constant, if we increase the likelihood numerator and denomenator by say a factor of F, we keep the same rate of successfully navigating an asteroid field (ie. F*num/F*den = num/den), but effectively increase the sample size. What then happens to the value of p? What happens is that the likelihood swamps the prior, and as F increases, the posterior becomes the likelihood. For example, if F=5, then p=.35. If F=100, then p=.026. If F=50000, then p=.00032. If F=250000, then p=.00028. As F increases, p tends towards alpha/(alpha+beta) or 2/(2+7440) = .000269. The remarkable thing is that this will occur for almost any prior we dream up.

Count Baysie concludes by saying that "This post has been pretty light on math, but the real aim was to introduce the idea of Bayesian Priors and show that they are as rational as believing that Han Solo isn't facing certain doom by entering the asteroid field. At the same time we can't just throw away the information that C3PO has to share with us." Actually, we should probably throw away the prior! We could argue, C3PO's likelihood is correct, and in real life Han Solo would most likely not make it.

Check out this Excel file to explore the posterior as changes to the likelihood and prior are made in this example, like in the screenshots above.

Thanks for reading.