Golf Putting Models

6/25/18

In Gelman and Nolan's A Probability Model for Golf Putting, they discuss an interesting geometric model to explain the putting performance of professional golfers. The data come from Don Berry's book "Statistics: A Bayesian Perspective". Gelman also has slides and video (starting at 47min, but the entire video is worth watching) where he discusses this dataset and models and conclusions.

Here is the main slide from the analyses. The red line is from a standard logistic regression. The blue line is from their geometric model.

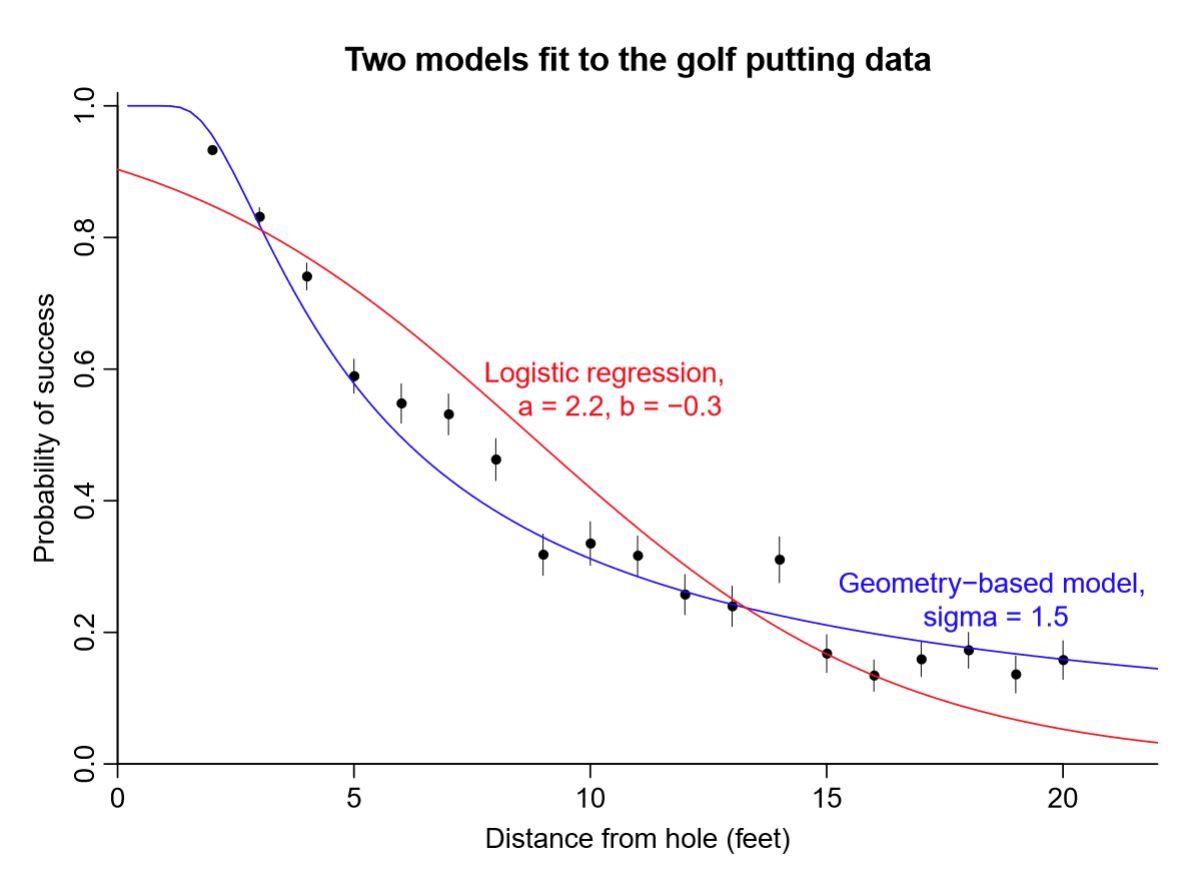
In the video, Gelman said

It [the logistic regression-J] incorrectly says that the probability of...it underestimates the probability of sinking a 0 ft putt, which of course would be 100%. On the other end, interestingly enough it also underestimates the probability of fitting [making-J] a difficult putt.

He also said

Our model has only 1 parameter and it beats the 2 parameter model [logistic regression-J].

and

It [his geometric model-J] correctly shows that golfers are still doing ok there [where distances are large-J].

Hmmm. First, we don't know what is "correct" and "incorrect". Second, I'm not sure why I'd want to force the probability of making a put shorter than 2 ft to be near or at 100% as their geometric model does. I'd also be curious if their model is overestimating the probability of making a longer or more difficult putt.

A few days ago, I sent him an email:

Hi Mr. Gelman,

Just going through some stuff on your site and came across the putting data.

In your article in Teaching Statistics, you say

"Also, shots from a zero distance must go in, and so the success probability at distance 0 must be 1."

Can we say that? That is, if the data was collected/measured in ft, is "0" a literal 0 ft, or does "0" just mean less than a foot, so it could still equate to some inches?

I ask because I think it matters in how the logistic regression is rejected as an inappropriate model since the y value is not at 100% for x=0. And being a former golfer myself, I know that a distance of a few inches even, golfers get the "yips" and miss those, so I would think 100% is not realistic for distance=0,

Thanks,

He responded

Hi, yes, good point, I have no idea because there were no putts in these data with distances less than 2 feet.

I am not sure how to justify Gelman's, or anybody elses, unique and interesting models they come up with. It seems like there could be an infinite number of them, with their own assumptions, parameters, hyper parameters, etc., to choose from, and they could all fit data well. However, I do know how to justify the general idea of a basic logistic regression model and then let the data do all or most of the talking. This is similar to the issue of defending priors in a Bayesian analysis.

While his model may have fewer parameters than in the logistic regression, there are many less assumptions going into the logistic regression than in his model. Which do you prefer? Note, we could use even less assumptions and parameters by doing a nonparametric regression.

Thanks for reading.

Note, as of 2019, there is new data and hence new models. See Gelman's article, as well as the data and models being included in Stan case studies. I note that the differences between the old and new data are quite dramatic. I believe the new data is from professionals and is also probably better measured. I still prefer the logistic models. In my opinion, the Bayesian models fit the data objectively better, but to the point of overfitting. One would also need to see a thorough sensitivity analysis on any priors and geometric models used.