Frequentism, or How the World Works
3/10/12
Frequentism, which is one way of defining and understanding probability, is incredible in its simplicity and power. This is an article to share the main ideas of frequentism. Also, be sure to read work by John Venn (The Logic of Chance), Richard von Mises (Probability, Statistics, and Truth), and more recently, Deborah Mayo (Statistical Inference as Severe Testing).
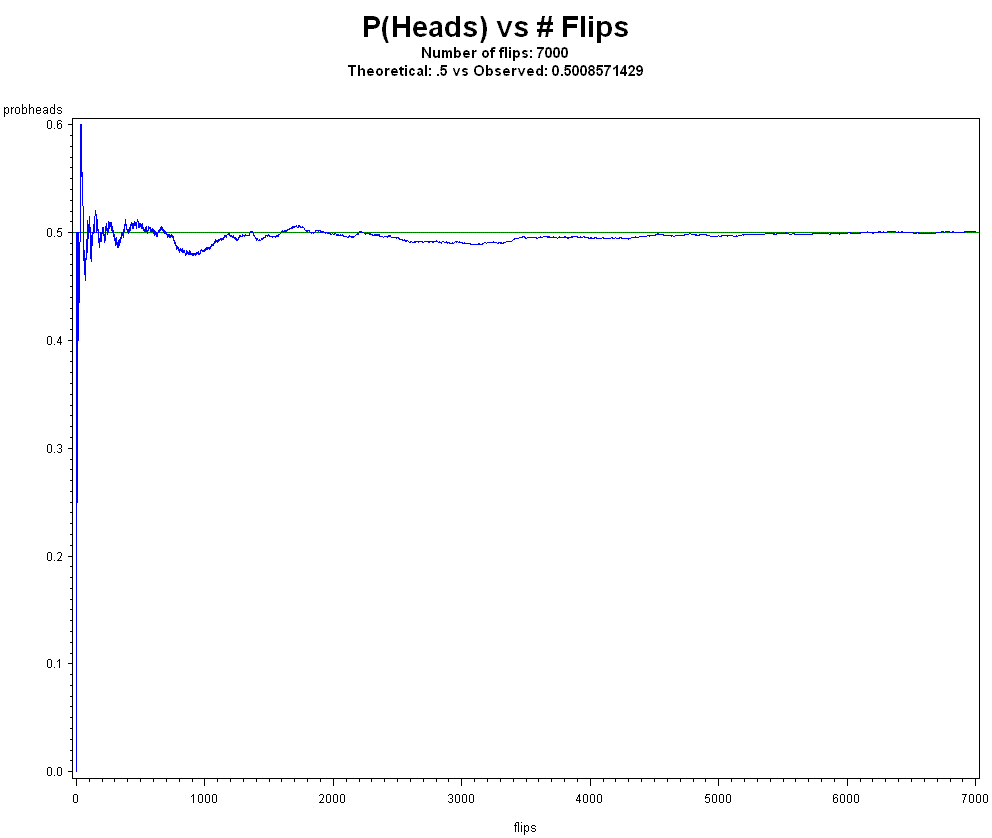
What do you believe will happen to the frequency of Heads if we simulate flipping a coin 7,000 times? Actually, your beliefs of what may happen don't matter. Let's just do the experiment and see what happens.
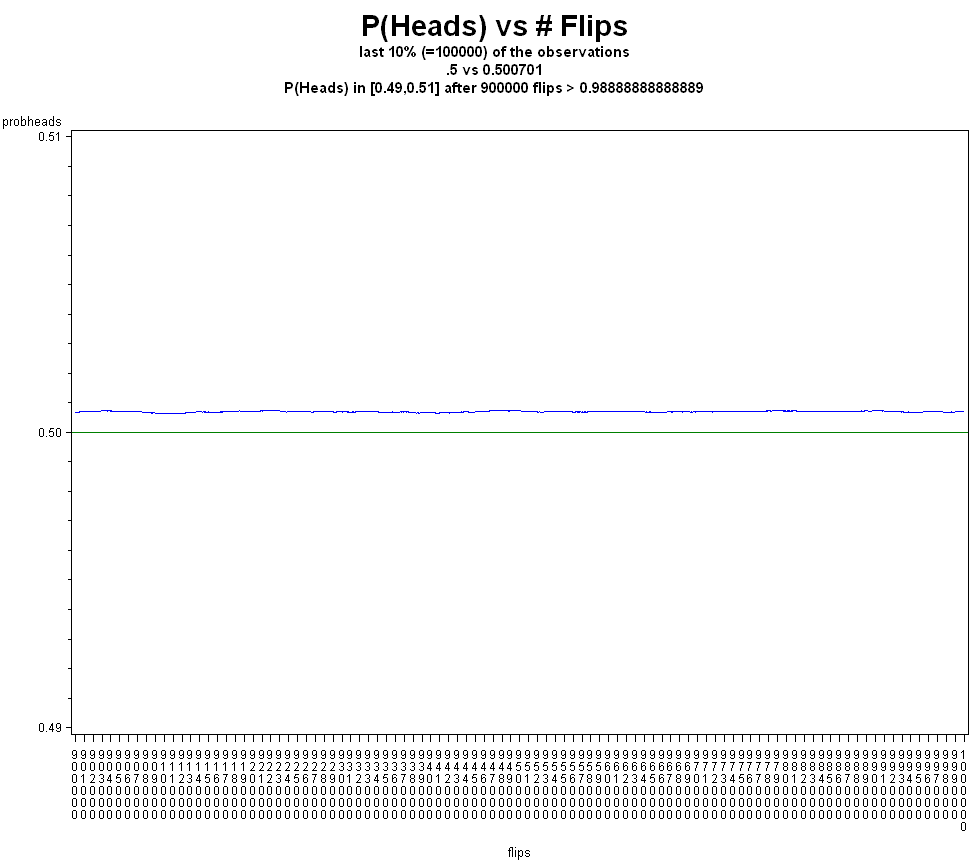
And how about 1,000,000 times?
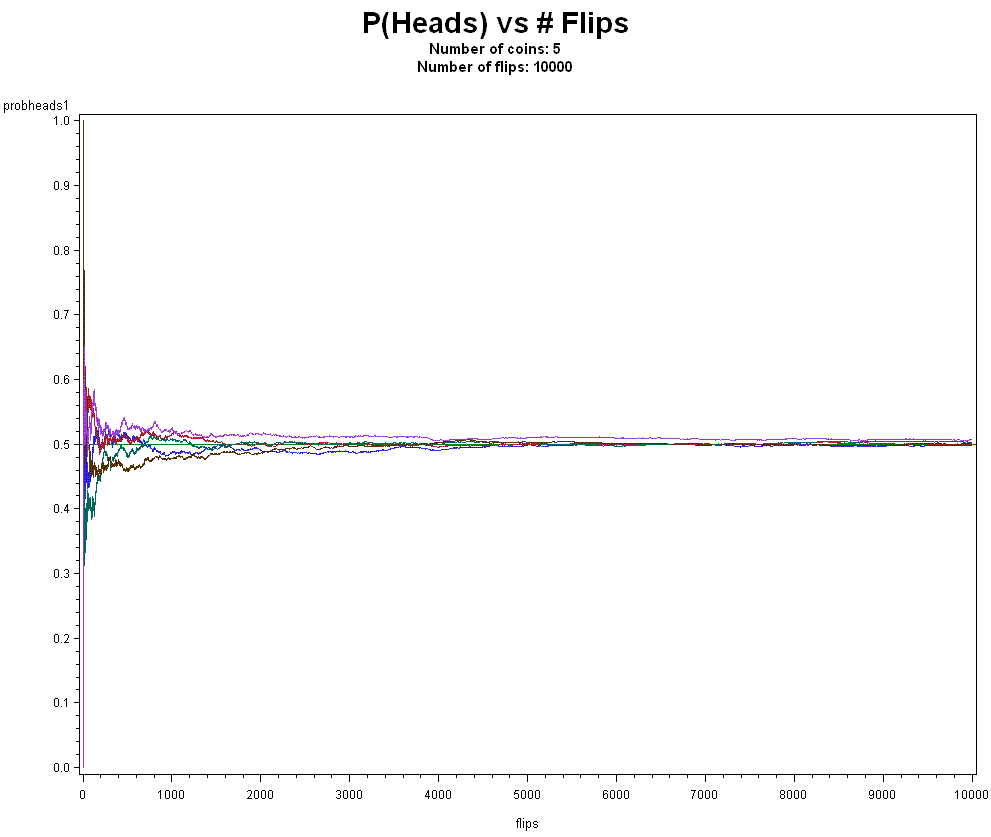
How about 5 coins 10,000 times?
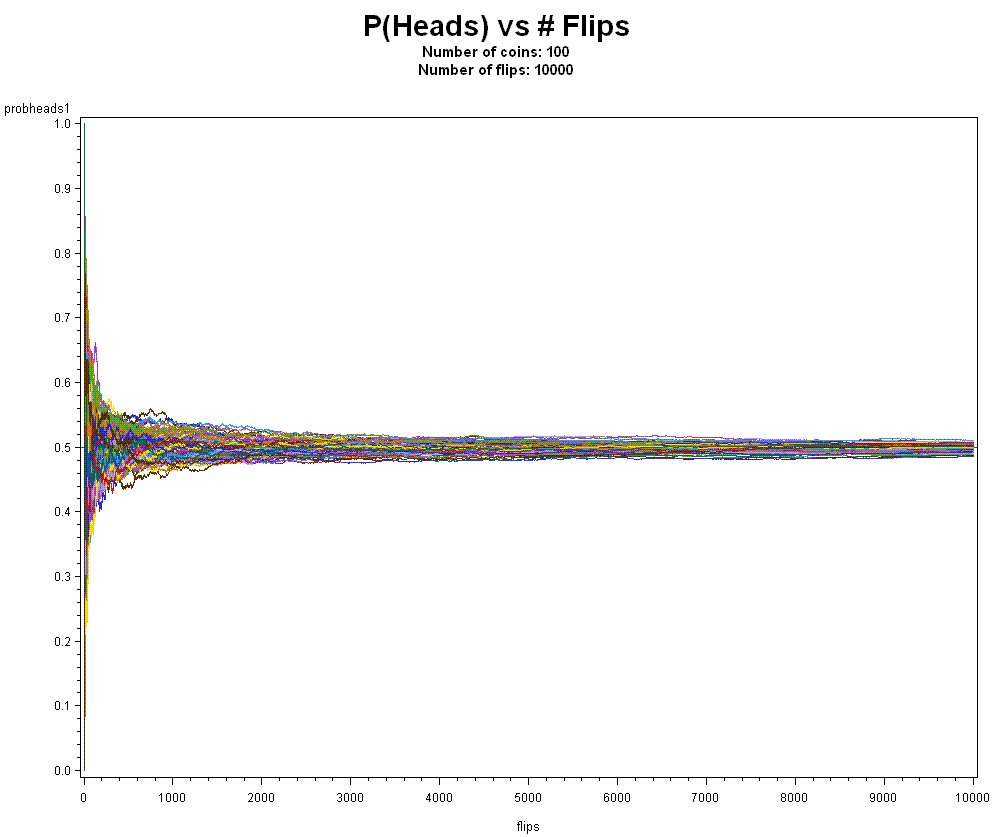
And how about 100 coins 10,000 times?
Much like the epsilon-delta proofs in calculus, one could ask someone "How close do you want to get?" to p. We could get them to within a small enough e that their measurement tool could not tell the difference, and this applies whether or not we know what the real p is.
The Strong Law of Large Numbers (SLLN) says that it is almost certain that between the mth and nth observations in a group of length n, the relative frequency of Heads will remain near the fixed value p and be within the interval [p-e, p+e], for any e > 0, provided that m and n are sufficiently large numbers. That is,
As an example, if we are going to flip a coin 1,000,000 times, and want to get within .01 of the true p (say .5 in this case), if we look at the last 100,000 flips (ie. flips 900,000 to 1,000,000) this tells us that
Could P(Heads) lie outside of this interval? Yes. Is that scenario likely? No.
Also, we shouldn't find frequentist p-values or confidence intervals confusing. Consider this graph
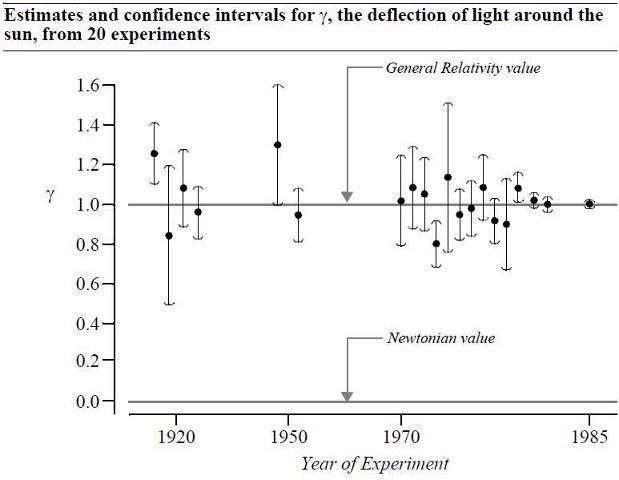
From the book Statistical Sleuth. Data originally from "General Relativity at 75: How Right was Einstein?" (Will, 1990)
Often, non-frequentist statistics rely on frequentism. For example, in some forms of Bayesian statistics, prior distributions often come from previous experiments. Also, sampling from the posterior distribution using Markov Chain Monte Carlo (MCMC) is frequentist. For example
- Use a burn-in period?
(make coin flips > some small number, since relative frequency is "rough" for a small number of flips) - Use more iterations?
(flip the coin more times, you know it will have a better chance of convergence) - Use more chains?
(flip more coins, multiple evidence of converging is better evidence of existence) - Starting with a different seed?
(and if still converges with different seeds, this is like entering a 'collective' randomly and still getting the same relative frequency)
Summary
You have a real or hypothetical sequence, S, of observations (evidence). You look for an attribute, A, in S and are interested in P(A). We have experience of frequency concepts with lotteries, casinos, coins, etc. (validation), so we know we can calculate the relative frequency of A as the number of occurrences of A (#A) divided by the length of S (n), to get #A/n (practicalness). For n = 1, all #A/n start at 0 or 1, which isn't too useful. If n is too small, #A/n tends to be unreliable (recognizing need for replication). If S is too small, we may choose a new S that contains our old one (collapsing). If n is large, on the other hand, #A/n often doesn't change beyond some decimal point (constancy). As n gets larger and larger, we often say P(A) ~ #A/n (reasonableness), and maintain that P(A) in [p-e, p+e] > 1 - 1/(m*e2), and P(A) = lim n->oo #A/n (theoretical justifications). This limit must exist for subsequences in S, no matter how you form the subsequences (randomness). Frequentism and other methods tend to converge to the same result and/or conclusion as n gets larger (convergence of methods). Compare this reasoning to Calculus, with its derivatives and integrals, being entirely based on limits (analogy). Because of these things, no one has to take our word for any P(A) - they can just use these devices themselves (replication, objectivity). Other methods, including Bayesian statistics, rely on frequentism for justification (gold-standard, adoption). We learn how the world works and make good long-term decisions based on frequentism and statistical tests from frequentism (error philosophy).Please anonymously VOTE on the content you have just read:
Like:Dislike: