Bayesianly Wrong

4/30/21

Count Bayesie, whom I responded to before in A Closer Look at Han Solo Bayes, recently wrote Technically Wrong: When Bayesian and Frequentist methods differ. In that article, he looks at confidence intervals for a proportion. However, he also rehashes many fallacies about frequentism. I write about these and many others in Objections to Frequentism.

Please check out his book Bayesian Statistics the Fun Way: Understanding Statistics and Probability with Star Wars, LEGO, and Rubber Ducks

On with my response.

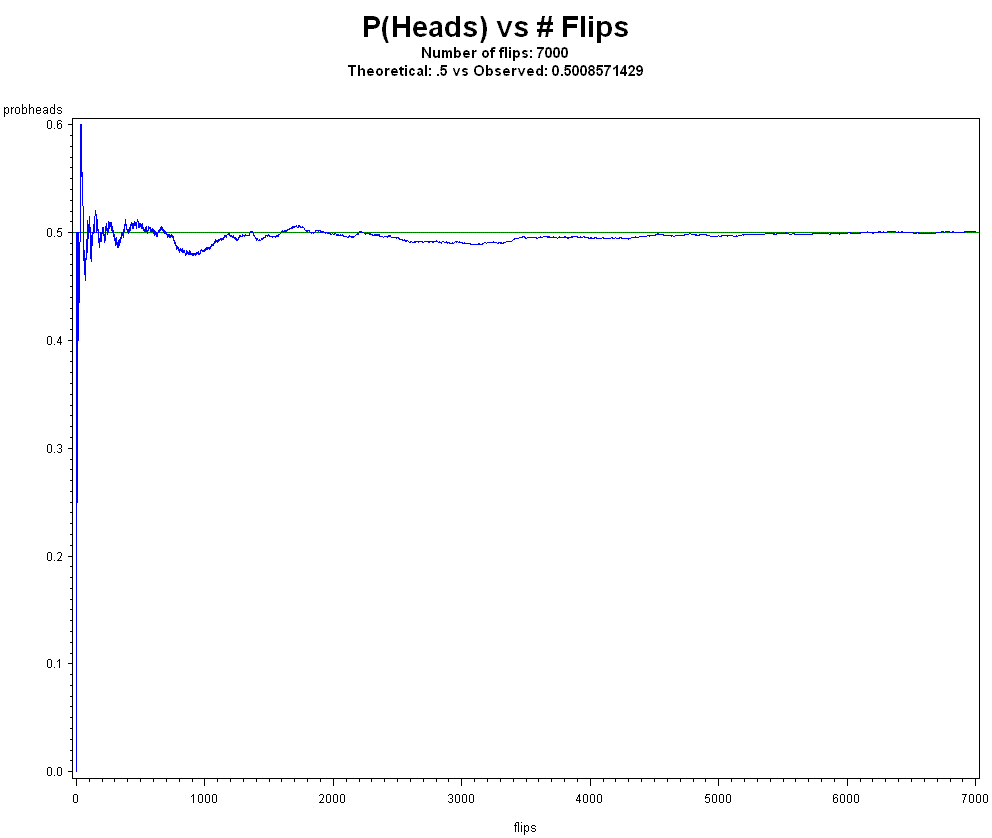
First, he obviously wants to equate "probability" with "belief". However, much like geologists don't specialize in bones, and paleontologists don't specialize in rocks, although there is some overlap in knowledge and techniques, "probability" and "uncertainty" (or "chance" or "belief") are distinct concepts. If you believe a coin has p=.80 of landing heads, that is interesting psychologically, but irrelevant to what the probability actually is as obtained from a well-designed experiment, where we would see the relative frequency of heads settle down to a straight line. No objections if the "prior" came from a well-designed experiment or survey, but this can be incorporated in the data itself, likelihood, modelling, or meta-analysis.

For example, the Strong Law of Large Numbers (SLLN) says that it is almost certain that between the m^th and n^th observations in a group of length n, the relative frequency of Heads will remain near the fixed value p, whatever p may be (ie. doesn't have to be 1/2), and be within the interval [p-e, p+e], for any small e > 0, provided that m and n are sufficiently large numbers. That is, P(Heads) in [p-e, p+e] > 1 - 1/(m*e²).

Second, he commits the "Statistician's Fallacy". This "what we really want to know (or say), is X" has been called "The Statistician's Fallacy" by Lakens. That is, statisticians saying what all researchers supposedly want to know, and not coincidentally the answer X is aligned 100% with the statistician's philosophy of statistics and science. For example

"You want to know on your next pull of the trigger, what is the probability it will fire."
"What we want to do is model our beliefs in possible values for the rate of fire.."
"what we want to do is come up with a distribution of what we believe the true rate could be..."
"When we plot out the distribution of our beliefs.."
"If you had never heard of statistics ... you would ... come to the Bayesian conclusion for the best estimate of the distribution of our beliefs given the observations we saw, even if you had never heard of Bayesian statistics."

When I do statistics, I do not seek to model beliefs. I seek to estimate something about a population using an experiment or sample using beliefs (in the very specific form of putting probability distributions on parameters) as little as possible, that is as objective as possible, robust to mistakes, and has good error control.

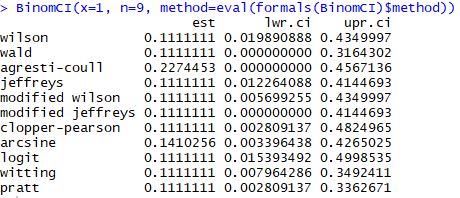
Third, he critiques a frequentist approach (large sample normal approximation) in a n = 9 case. This just shows that he is either unaware of the assumptions involved with using this method, or shows what can go wrong if one doesn't check the assumptions required to use a method. One would need to have something like np > 5 or 10, n>30, guidance on alpha and beta, or whatever a sensible rule of thumb is to use a large sample normal approximation.

Fourth, he tries to sell "ad hoc" as being something bad and "magical thinking". However, "ad hoc" just means "as needed" or "done for a particular purpose", which is quite sensible. Frequentist methods are free and not tied down to any single approach. Therefore, frequentist methods don't suffer from "every problem requires the same tool" (ie. Bayes rule), which can be extremely limiting. In fact, he repeatedly uses "ad hoc" to limit the very valid point that there are many other frequentist (and other) methods that perform better than a large sample normal approximation does in a n = 9 case, referring to these ways to solve distinct problems as a "catalog of tricks". Some of these methods are: Clopper-Pearson, Wilson, Wald, Agresti-Coull, arcsine, logit, Witting, Pratt, mid-p, likelihood-based, Blaker, and others. In addition, there are a variety of bootstrap methods for a confidence interval of a proportion.

Fifth, he tries to deflect from the problems of priors. It is very real that peoples' priors can not only differ, but differ dramatically enough to reach completely opposite conclusions (so there is no "the" probability or "the" prior). Moreover, there can be massive false confidence, as well as priors can be overly subjective and brittle. Last, for large n or as n/N goes to 1, likelihoods typically swamp priors and therefore priors/beliefs show their irrelevancy. Not to mention, there is hardly any agreement among Bayesians on how to choose priors, and all Bayesian analyses probably should be accompanied by a sensitivity analysis to see what could have happened had different beliefs been convoluted with the likelihood.

Sixth, in his example, he denies the frequentist to use their knowledge of the real world. For example, even using the normal approximation, which is inappropriate here, a frequentist would not use a in a confidence interval [a,b] if a<0, because they know about the real world. I would argue, however, that having to make a=0 if a<0 (or make b=1 if b>1) is a good tradeoff to get rid of using subjective priors. He calls the values less than 0 "impossible", but discounts the fact that some beliefs may be impossible as well.

Seventh, saying frequentist methods are "technically wrong" itself is wrong. He claims that "We didn't derive this formula [the frequentist one using normal approximation] from probability theory properly, but rather by throwing together a few mathematical tools that look right together in an ad hoc manner". In reality, every one of the equations for the confidence interval for a proportion were derived in a rigorous manner to solve distinct problems. It just happens that he misapplied one of these, maybe for dramatic effect.

Some concluding thoughts

Conjugate priors are only used in simple settings and often for convenience. In practice, Markov Chain Monte Carlo (MCMC) is used to obtain posterior distributions, which paradoxically relies heavily on frequentism to get results.

In his example, the Bayes estimator can be rewritten as a weighted average of the observed proportion of successes (b/n) and the prior belief (E(p)=r/(r+s)):

E(p|B=b) = (n/(n+r+s))*(b/n) + ((r+s)/(n+r+s))(r/(r+s))

or even more precisely, since priors are hardly agreed upon

E(p|B=b) = (n/(n+r+s))*(b/n) + ((r+s)/(n+r+s))(Count Bayesie's Belief)

As n gets large, the second term tends to 0 and the first term tends to b/n. And obviously as n gets large, as n/N goes to 1, we learn how things really are (given a sensible likelihood and well-designed experiments/surveys anyway).

Moreover, the Bayesian approach of using a beta-binomial conjugate prior is simply equivalent to adding a certain number of pseudo-observations to the dataset and analyzing the resulting dataset using standard frequentist methods. In light of this fact, the use of a prior then "blessing" Bayesians to talk about probability claims, yet frequentists are denied this, therefore doesn't make much sense.

The prior should also have support on the entire parameter space. For example, if you put a uniform prior on [0,1/2], and the true p is greater than 1/2, the Bayesian procedure will not converge to the true value. Or if one truly believes p=0 or p=1, then then Bayesian estimate cannot inform you. These demonstrate that some beliefs are more valid than others.

Count Baysie may "spend very little time near infinity" (don't we all?) so doesn't see the need for asymptotic arguments, but frequentists probably spend very little time around small n for good reason, and approximations (we're really talking about mathematical convergence!) get good fast, even for moderate n. Sometimes even for small n, the frequentist procedure can be better because it isn't being potentially biased by priors and more assumptions.

If your goal is to always focus on "probability" (well, you're approximating P(H₀) by P(H₀|your beliefs) anyway), always using the same tool, then you may be a "probabilist" or a "Bayesian maximalist". However, being able to compute something like a probability for H₀ does not mean H₀ was well-tested at all, which seems more important. For more information on the latter and related topics, please see Statistical Inference as Severe Testing: How to Get Beyond the Statistics Wars by Mayo

Thanks for reading.