Barbell Tipping

12/12/11

In bodybuilding/strength training forums I regularly read this question "How much weight can I add to one side of a racked barbell before it tips over?" There are a lot of simplifying assumptions one can make to tackle this problem, and here is a general idea. Statics experts (of which I am not one) - please write in!

Let a racked barbell that weighs B lbs have its supports at x₁ and x₂. Say there is m₁ lbs at x₁ and m₂ lbs at x₂. The center of mass of the unweighted barbell itself is at d/2, where d is the length of the barbell.

Note that for a bar to not be tipping, it is not rotating about a support. Therefore the sum of the torque equals zero. Mathematically, for an arbitrary point X, this is

Note that if sum(torques) = 0, this implies that X = X_cm (center of mass), and

I've ignored the weight, B lbs, of the bar here. Adding that back in, we get

So when will the barbell tip over? Without loss of generality, assume we are just adding weight to m₁. The bar will then tip when X_cm < x₁. That is, when the center of mass is outside of the support. The situation is:

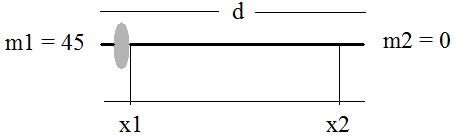
Note something interesting here. Because each weight plate has a thickness, the new x₁ point that we are loading with mass is actually shifting to a number smaller than x₁ as we add additional weight to the bar. So we're not just adding more weight, but adding more weight further from the support.

If I substitute in specific numbers, these tend to match reality pretty well. For around 3 to 3+ plates it tends to tip for the setups I've used if there are no plates on the other side (ie. m₂ = 0). Here's a setup with some hypothetical numbers:

• B = 45 lbs
• bar's center of mass = d/2 = 42 inches
• starting m₁ = 45 lbs
• m₂ = 0 lbs
• starting x₁ = 24 inches
• x₂ = 60 inches
• assume x₁ shifts 3 inches to the left of the starting x₁ with each plate added

Note that for 1 and 2 plates added to m₁, X_cm is still greater than 24 inches (the original x₁). However, when a little over 3 plates are added, X_cm < 24, and therefore tipping occurs.

In practice, however, I'd recommend to not ever have the difference between m₁ and m₂ be large at all. Actually, there's really no need to use a barbell in the first place.